今回はコーシーリーマンの方程式と微分可能性について解説していきます。
前回の記事は複素関数の導関数についてで、複素平面上でも実数と同じように微分の考えを適応できるという話をしました。
そして、複素関数が実関数と異なるのは、極限が方向によらないということでした。
このことから微分可能な複素関数の条件を考えることができます。
それが「コーシー・リーマンの方程式」です。
目次
コーシー・リーマンの方程式
$$f\left(z\right)=f\left(x+iy\right)=u\left(x, y\right)+iv\left(x, y\right)がz=z_0で微分可能である時、$$
$$導関数f'\left(z_0\right)は、$$
前回の記事で定義したように、以下のように書けます。
$$f'\left(z_0\right)=\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$この時、実関数u, vは、点z=z_0=x_0+iy_0において、以下の式を満たします。$$
$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}, \enspace\enspace \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$
$$これらの関係式をコーシー・リーマンの方程式と言います。$$
コーシー・リーマンの方程式の証明
証明には複素関数の導関数の式を使います。
$$複素関数の導関数$$
$$f'\left(z_0\right)=\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$この式にf\left(z\right)=f\left(x+iy\right)=u\left(x, y\right)+iv\left(x, y\right)、z_0=x_0+iy_0, Δz=Δx+iΔyを代入します。$$
$$f'\left(x_0+iy_0\right)=\lim_{Δx+iΔy\to 0}\frac{u\left(x_0+Δx, y_0+Δy\right)+iv\left(x_0+Δx, y_0+Δy\right)-u\left(x_0, y_0\right)+iv\left(x_0, y_0\right)}{Δx+iΔy}・・・①$$
ここで、二つの近づき方の極限を考えます。「実軸に平行に近づく極限」と「虚軸に平行に近づく極限」の二つです。
$$複素関数の極限は方向によらないので、どの方向からz=z_0に近づこうとも同じ値になるということを利用して、$$
$$コーシー・リーマンの式を導きましょう。$$
「複素関数の極限は方向によらない」については、「(複素数の極限について)」でその理由を詳しく説明しています。
$$(i) 実軸に平行に近づく極限$$
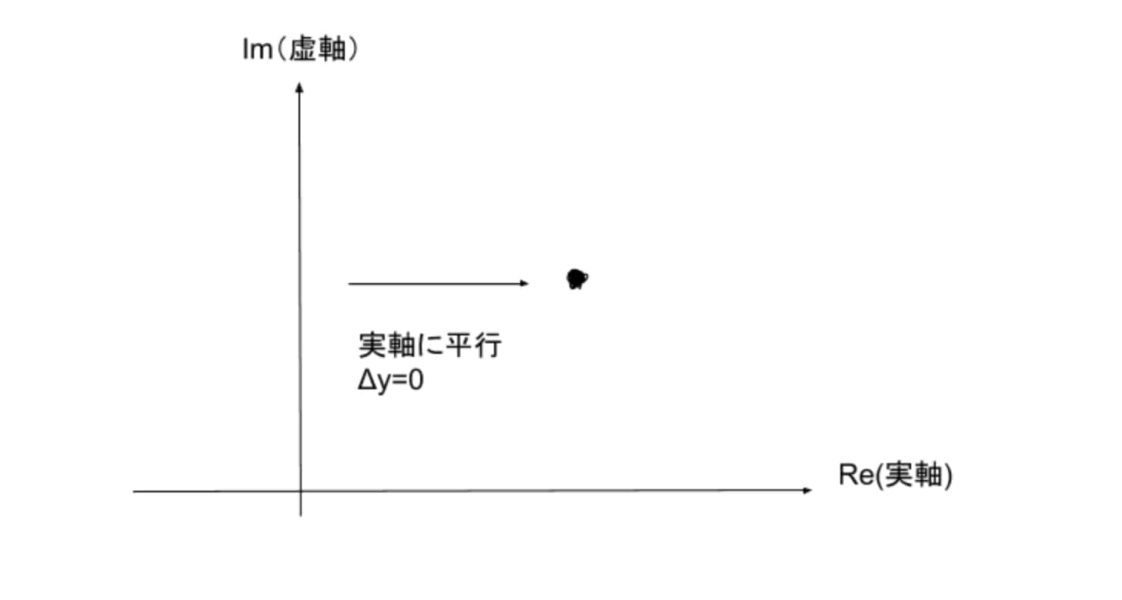
$$図を見ても分かる通り、Δyは、虚軸方向の変化なので、Δy=0ですね。$$
$$そして実軸に平行にz=z_0に近づくので、Δx\to 0として考えます。$$
$$①より、$$
$$f'\left(z_0\right)=\lim_{Δx\to 0}\frac{u\left(x_0+Δx, y_0\right)+iv\left(x_0+Δx, y_0\right)-u\left(x_0, y_0\right)+iv\left(x_0, y_0\right)}{Δx}$$
$$=\frac{\partial u\left(x_0, y_0\right)}{\partial x} + i\frac{\partial v\left(x_0, y_0\right)}{\partial x}・・・②$$
とできました。(この変形は、偏微分の定義式から考えられますね。)
$$f'\left(z_0\right)は、xの偏微分で計算できるんですね。$$
$$(ii)虚軸に平行に近づく極限$$
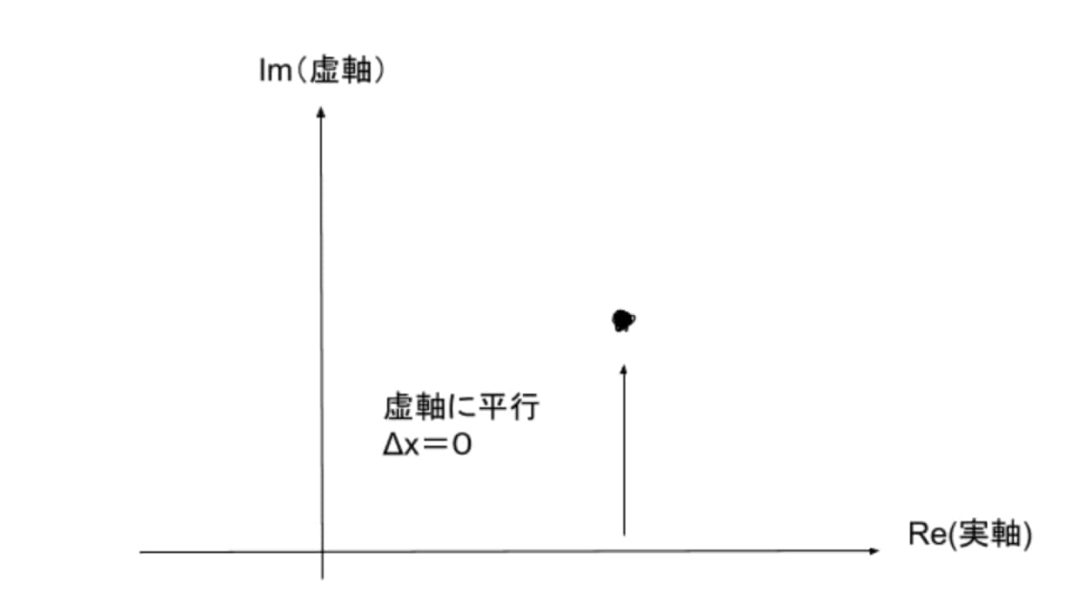
$$こちらも(i)と同様に、図を見ても分かる通り、Δxは、実軸方向の変化なので、Δx=0ですね。$$
$$そして虚軸に平行にz=z_0に近づくので、Δy\to 0として考えます。$$
$$①より、$$
$$f'\left(z_0\right)=\lim_{Δy\to 0}\frac{u\left(x_0, y_0+Δy\right)+iv\left(x_0, y_0+Δy\right)-u\left(x_0, y_0\right)+iv\left(x_0, y_0\right)}{Δy}$$
$$=\frac{\partial v\left(x_0, y_0\right)}{\partial y} - i\frac{\partial u\left(x_0, y_0\right)}{\partial y}・・・③$$
$$なるほどf'\left(z_0\right)は、yの偏微分でも計算できるんですね。$$
ここまでくると、ほぼ証明できましたね。
$$(i)(ii)でできた式②、③より、実部と虚部を比較して、$$
$$\frac{\partial u\left(x_0, y_0\right)}{\partial x}=\frac{\partial v\left(x_0, y_0\right)}{\partial y}、\frac{\partial u\left(x_0, y_0\right)}{\partial y}=-\frac{\partial v\left(x_0, y_0\right)}{\partial x}$$
$$となって、見事コーシー・リーマンの式が出てくれました。$$
上の証明からも分かる通り、「複素関数の極限が方向によらない」という特徴を持っているからこの式が存在できるのですね。存在すべきというべきでしょうか。
コーシー・リーマンの方程式と微分可能性
ここまで、コーシー・リーマンの方程式について述べてきましたが、ここからは、コーシー・リーマンの方程式と微分可能性の関係について述べていきたいと思います。
これまでの話を思い出していただくと、
$$「ある複素関数が微分可能である時、その複素関数の実部と虚部はコーシー・リーマンの方程式を満たす」$$
ということでした。
そして、今回説明するのは、
$$「ある複素関数f\left(z\right)=u\left(x, y\right)+iv\left(x, y\right)について、\frac{\partial u}{\partial x}、\frac{\partial u}{\partial y}、\frac{\partial v}{\partial x}、\frac{\partial v}{\partial y}が存在し、$$
$$かつコーシー・リーマンの方程式が成立する時、f\left(z\right)はz=z_0において、微分可能である。」$$
今までのが「微分可能ならコーシー・リーマンを満たす」だったのに対し、今回は「コーシー・リーマンを満たすなら微分可能」ということですね。
それでは証明していきます。
$$証明$$
$$複素関数の導関数は$$
$$f'\left(z_0\right)=\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
でした。
$$ここで、分子のf\left(z_0+Δz\right)-f\left(z_0\right)について考えます。$$
$$Δzは、複素数zの変化を表すので、Δz=z-z_0 \to z=Δz+z_0です。$$
$$よって、f\left(z_0+Δz\right)-f\left(z_0\right)=f\left(z\right)-f\left(z_0\right)ですね。$$
$$f\left(z\right)-f\left(z_0\right)=u\left(x, y\right)+iv\left(x, y\right)-u\left(x_0, y_0\right)+iv\left(x_0, y_0\right)$$
$$この式をコーシー・リーマンの関係式を使ってうまく変形し、$$
$$複素関数の導関数の式に代入してちゃんとf'\left(z_0\right)の形になることを確かめます。$$
$$f\left(z\right)-f\left(z_0\right)=\frac{\partial u\left(x_0, y_0\right)}{\partial x}Δx+\frac{\partial u\left(x_0, y_0\right)}{\partial y}Δy+i\left(\frac{\partial v\left(x_0, y_0\right)}{\partial x}Δx+\frac{\partial v\left(x_0, y_0\right)}{\partial y}Δy\right)+O\left(\left(Δz\right)^2\right)$$
$$この変形につきましては、u\left(x, y\right)とv\left(x, y\right)の近似をしています。これは下の補足で解説しています。$$
$$ここで、コーシー・リーマンの関係式より、$$
$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}、\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$
$$f\left(z\right)-f\left(z_0\right)=\frac{\partial u\left(x_0, y_0\right)}{\partial x}\left(Δx+iΔy\right)+i\frac{\partial v\left(x_0, y_0\right)}{\partial x}\left(Δx+iΔy\right)+O\left(\left(Δz\right)^2\right)$$
$$=\left(\frac{\partial u\left(x_0, y_0\right)}{\partial x}+i\frac{\partial v\left(x_0, y_0\right)}{\partial x}\right)Δz+O\left(\left(Δz\right)^2\right)$$
$$この式を複素関数の導関数の式に代入します。$$
$$f'\left(z_0\right)=\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$=\lim_{Δz\to 0}\frac{1}{Δz}\left(\left(\frac{\partial u\left(x_0, y_0\right)}{\partial x}+i\frac{\partial v\left(x_0, y_0\right)}{\partial x}\right)Δz+O\left(\left(Δz\right)^2\right)\right)$$
$$=\frac{\partial u\left(x_0, y_0\right)}{\partial x}+i\frac{\partial v\left(x_0, y_0\right)}{\partial x}=f'\left(z_0\right)$$
$$となり、z=z_0において微分可能であることが証明されました。$$
証明はかなりかいつまんでしました。下の補足のところで、証明について詳しく書いてあり、そこを読んでいただければ、不明点が解決するはずです。ぜひ読んでみてください!
$$補足1(u\left(x, y\right)とv\left(x, y\right)の近似)$$
$$実関数であるu\left(x, y\right)とv\left(x, y\right)をテーラー展開します。$$
$$私は大学一年の初期に一応習ったらしいのですが、そんなものは知りません。$$
$$なので、そういったものがあるのかと理解は後回しで進めていきました。$$
$$(ちゃんと理解しようとすれば簡単です。テーラー展開はローラン級数のところで解説します。)$$
$$テーラー展開$$
$$f\left(x\right)=f\left(x_0\right)+f'\left(x_0\right)Δx+\frac{1}{2!}f''\left(Δx\right)^2+・・・・$$
$$(多くのサイトや参考書には、Δxのところは、x-x_0等で書かれてます。)$$
上の式を参考に、
$$u\left(x, y\right)=u\left(x_0, y_0\right)+\frac{du\left(x_0, y_0\right)}{dz}Δz+\frac{1}{2!}\frac{d^2u}{du^2}\left(Δz\right)^2+・・・$$
詳細にみてみましょう。
$$\frac{du\left(x_0, y_0\right)}{dz}Δzについて$$
$$\frac{du\left(x_0, y_0\right)}{dz}は全微分なので、\frac{du\left(x_0, y_0\right)}{dz}=\left(\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy\right)\frac{1}{dz}と書けます。$$
$$\lim_{Δz\to 0}Δz=dzなので、(変化量Δzを微小にしたらdz)$$
$$\frac{du\left(x_0, y_0\right)}{dz}Δz=\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy=\frac{\partial u}{\partial x}Δx+\frac{\partial u}{\partial y}Δy$$
$$(変化量Δx, Δyが微小な時、dx, dyと等しいです。)$$
$$v\left(x, y\right)についても同様に計算すると$$
$$v\left(x, y\right)=\frac{\partial v\left(x_0, y_0\right)}{\partial x}Δx+\frac{\partial v\left(x_0, y_0\right)}{\partial y}Δy$$
とできます。
$$補足2(O\left(\left(Δz\right)^2\right)とは)$$
$$次にO\left(\left(Δz\right)^2\right)について$$
O()は、オーダー記法(ランダウの記号)といい、関数の中の誤差として評価できる項を、だいたいこんな感じと書いてしまう記法です。
どういうことでしょうか。
例を見た方が早そうです。
$$\left(x+Δx\right)^3=x^3+3xΔx+3x\left(Δx\right)^2+\left(Δx\right)^3について$$
$$\left(x+Δx\right)^3=x^3+3xΔx+3x\left(Δx\right)^2+O\left(\left(Δx\right)^3\right)$$
$$\left(x+Δx\right)^3=x^3+3xΔx+O\left(\left(Δx\right)^2\right)$$
$$\left(x+Δx\right)^3=x^3+O\left(Δx\right)$$
$$\left(x+Δx\right)^3=O\left(1\right)$$
「まあなんとなくどんなものかはわかったけども。。」という感じですね。
今回はそれで十分だと思います。
$$上の証明で出てきたO\left(\left(Δz\right)^2\right)は、Δzの関数なので、$$
$$極限でΔz\to 0に飛ばしたので、O\left(\left(Δz\right)^2\right)が0になったのですね。$$
まとめ
いかがでしたでしょうか?
今回はコーシー・リーマンの方程式と微分可能性について解説しました。
今回の話は、次回でお話しする「複素関数」の分野でとても重要な「正則関数」で、重要な役割を果たします。
ここまでご覧いただきありがとうございました!