今回はローラン級数について解説します。
目次
ローランの定理
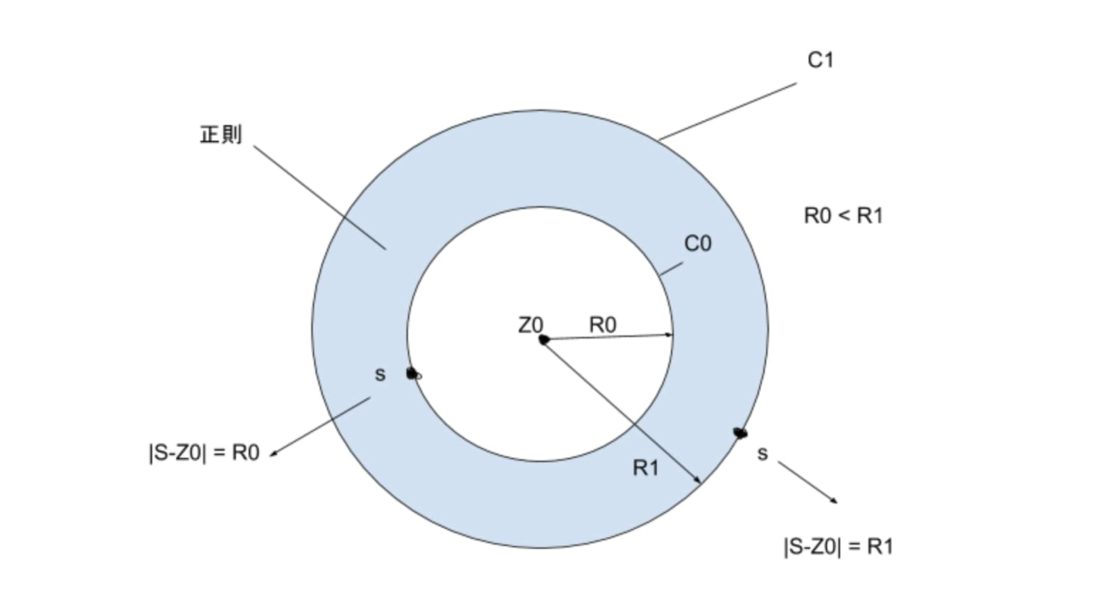
$$図のように、$$
$$z_0を中心とする同心円のC_0(半径R_0)、$$
$$C_1(半径R_1)を考えます。$$
$$その円環領域で複素関数f\left(z\right)が正則なとき、$$
$$円環領域内の任意の点zにおいてf\left(z\right)は、$$
$$f\left(z\right)=\displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}+\displaystyle\sum_{n=1}^{\infty}{\frac{b_n}{\left(z-z_0\right)^n}}$$
のように展開できます。一項目(正のべき)を正則部、二項目(負のべき)を主要部と言います。
$$また、a_n、b_nについて、以下の式で与えられます。$$
$$a_n=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(z\right)}{\left(z-z_0\right)^{n+1}}dz\enspace\enspace\enspace\enspace\left(n=0, 1, 2, ・・\right)$$
$$b_n=\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(z\right)}{\left(z-z_0\right)^{-n+1}}dz\enspace\enspace\enspace\enspace\left(n=1, 2, 3,・・\right)$$
ローランの定理 証明
$$証明$$
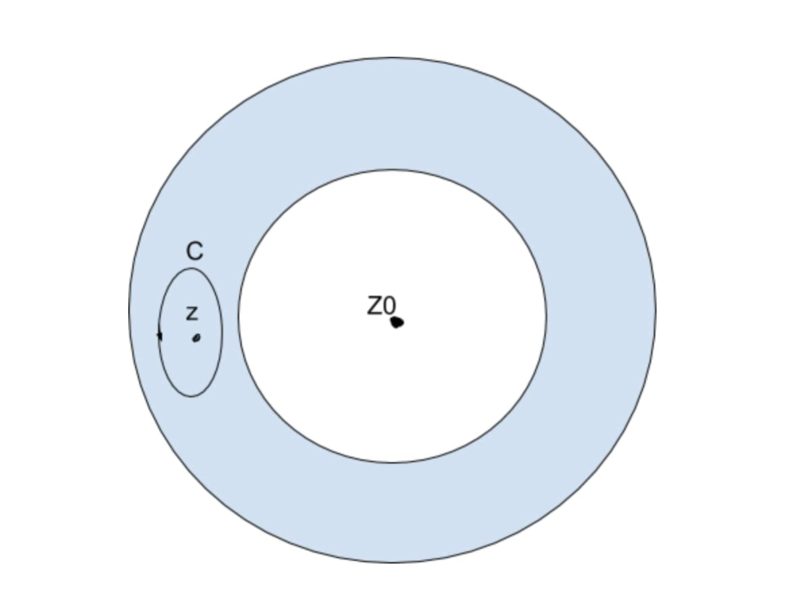
図のような経路Cを用いると、その領域では、
$$f\left(z\right)の正則なので$$
コーシーの積分公式より、
$$f\left(z\right)=\frac{1}{2\pi i}\displaystyle\int_C\frac{f\left(s\right)}{s-z}ds・・・①$$
また、コーシーの積分定理より、正則な領域内なら積分経路を自由に変形できました。
よって次のように経路を変形します。

$$図のように経路CをC_1+C_2-C_0+C_3に変形します。$$
$$C_0は経路が負の向きなのでマイナスがついています。$$
$$よって①より、$$
$$f\left(z\right)=\frac{1}{2\pi i}\displaystyle\int_{C_1+C_2-C_0+C_3}\frac{f\left(s\right)}{s-z}ds$$
$$=\frac{1}{2\pi i}\displaystyle\left[\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z}ds+\displaystyle\int_{C_2}\frac{f\left(s\right)}{s-z}ds-\displaystyle\int_{C_0}\frac{f\left(s\right)}{s-z}ds+\displaystyle\int_{C_3}\frac{f\left(s\right)}{s-z}ds\right]$$
$$=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z}ds-\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{s-z}ds・・・②$$
$$経路C_2とC_3は経路が十分に近く、$$
$$互いに方向が逆なので打ち消し合います。$$
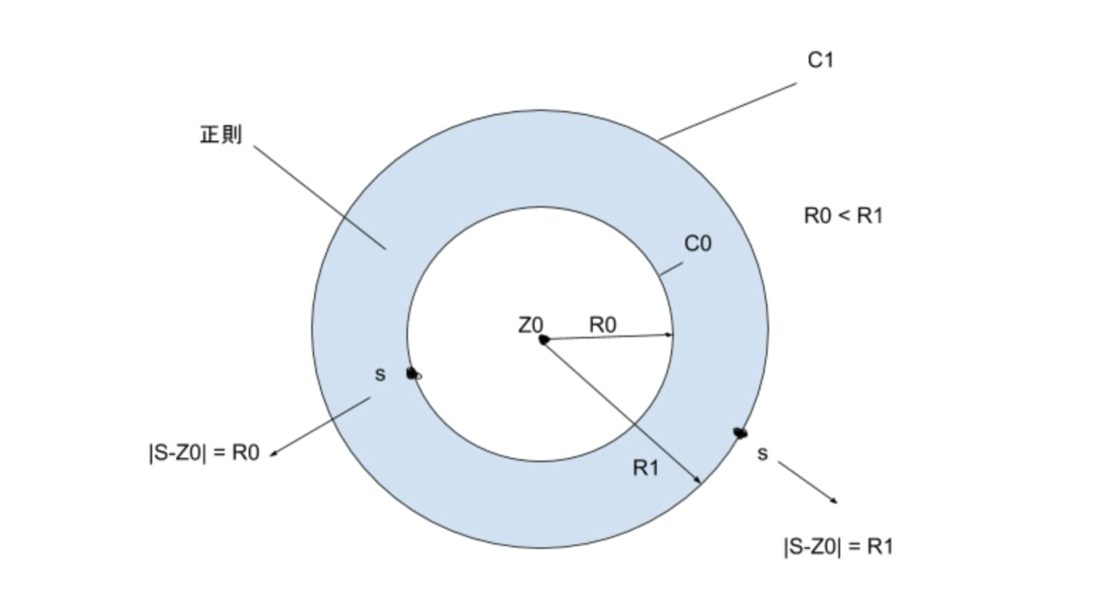
ここで、図を見てわかるように
$$経路C_1について、点zはC_1の内部にあり、$$
$$点sは|s-z_0|=R_1\left(円C_1の半径\right)なので、C_1上にあります。$$
$$よって、|z-z_0| < |s-z_0| \to \displaystyle|\frac{z-z_0}{s-z_0}| < 1が成り立ちます。$$
$$経路C_0について、点zはC_0の外部にあり、$$
$$点sは、|s-z_0| = R_0\left(円C_0の半径\right)なので、C_0上にあります。$$
$$よって、|z-z_0| > |s-z_0| \to \displaystyle|\frac{s-z_0}{z-z_0}| < 1が成り立ちます。$$
ここで、前回のテイラー展開の証明でもやったように無限等比級数の和
$$\displaystyle\sum_{n=0}^{\infty}r^n=1+r+r^2+・・・=\frac{1}{1-r}\enspace\enspace\left(|r| < 1\right)$$
を思い出してください。
$$経路C_1においては、\displaystyle|\frac{z-z_0}{s-z_0}| < 1、$$
$$経路C_0においては、\displaystyle|\frac{s-z_0}{z-z_0}| < 1$$
$$が成り立つので、②の式をうまく変形し、$$
$$無限等比級数の和の式を使えるようにしましょう。$$
$$②の\frac{1}{s-z}について$$
$$経路C_1において、$$
$$\frac{1}{s-z}=\frac{1}{s-z_0}・\frac{1}{1-\frac{z-z_0}{s-z_0}}$$
$$\displaystyle\left(=\frac{1}{\left(s-z_0\right)\left(1-\frac{z-z_0}{s-z_0}\right)}=\frac{1}{\left(s-z_0\right)-\left(z-z_0\right)}=\frac{1}{s-z}\right)$$
$$経路C_0において、$$
$$\frac{1}{s-z}=-\frac{1}{z-z_0}・\frac{1}{1-\frac{s-z_0}{z-z_0}}$$
$$\displaystyle\left(=-\frac{1}{\left(z-z_0\right)\left(1-\frac{s-z_0}{z-z_0}\right)}=-\frac{1}{\left(z-z_0\right)-\left(s-z_0\right)}=\frac{1}{s-z}\right)$$
とそれぞれ変形できます。
よって、無限等比級数の式より、
$$経路C_1において、\displaystyle|\frac{z-z_0}{s-z_0}| < 1なので$$
$$\frac{1}{1-\frac{z-z_0}{s-z_0}}=\displaystyle\sum_{n=0}^{\infty}\left(\frac{z-z_0}{s-z_0}\right)^n$$
$$経路C_0において、\displaystyle|\frac{s-z_0}{z-z_0}| < 1なので$$
$$\frac{1}{1-\frac{s-z_0}{z-z_0}}=\displaystyle\sum_{n=0}^{\infty}\left(\frac{s-z_0}{z-z_0}\right)^n$$
$$よって②より、$$
$$f\left(z\right)=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z}ds-\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{s-z}ds$$
$$=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z_0}\frac{ds}{1-\frac{z-z_0}{s-z_0}}+\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{s-z_0}\frac{ds}{1-\frac{s-z_0}{z-z_0}}$$
$$=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z_0}\displaystyle\sum_{n=0}^{\infty}\left(\frac{z-z_0}{s-z_0}\right)^n ds+\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{s-z_0}\displaystyle\sum_{n=0}^{\infty}\left(\frac{s-z_0}{z-z_0}\right)^n ds$$
$$=\displaystyle\sum_{n=0}^{\infty}\left\{\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{\left(s-z_0\right)^{n+1}}ds\right\}\left(z-z_0\right)^n+\displaystyle\sum_{n=1}^{\infty}\left\{\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{\left(s-z_0\right)^{-n+1}}ds\right\}\frac{1}{\left(z-z_0\right)^n}$$
$$ここで、$$
$$a_n=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{\left(s-z_0\right)^{n+1}}ds\enspace\enspace\enspace\enspace\enspace\left(n=0, 1, 2, ・・・\right)$$
$$b_n=\frac{1}{2\pi i}\displaystyle\int_{C_0}\frac{f\left(s\right)}{\left(s-z_0\right)^{-n+1}}ds\enspace\enspace\enspace\enspace\enspace\left(n=1, 2, 3, ・・・\right)$$
とおくと、
$$f\left(z\right)=\displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}+\displaystyle\sum_{n=1}^{\infty}{\frac{b_n}{\left(z-z_0\right)^n}}$$
とできました。
例題
$$(i)\frac{cosz}{z^3}をz=0を中心にローラン展開$$
$$coszを「z=0を中心にテイラー展開」(マクローリン展開)すると$$
$$cosz=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+・・・+\frac{\left(-1\right)^n}{\left(2n\right)!}z^{2n}+・・・$$
なので、
$$\frac{cosz}{z^3}=\frac{1}{z^3}\displaystyle\left\{1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+・・・+\frac{\left(-1\right)^n}{\left(2n\right)!}z^{2n}+・・・\right\}$$
$$=\frac{1}{z^3}-\frac{1}{2!}・\frac{1}{z}+\frac{z}{4!}-\frac{z^3}{6!}+・・・+\frac{\left(-1\right)^n}{\left(2n\right)!}z^{2n-3}+・・・$$
と展開できました。
$$\enspace$$
$$\enspace$$
$$\enspace$$
$$\enspace$$
$$(ii)f\left(z\right)=\frac{1}{z\left(z-i\right)}を、z=0を中心にローラン展開$$
$$z=0とiと2つが孤立特異点なので$$
$$(a)\enspace 0 < |z| < 1 と(b)\enspace 1 < |z|で場合分けします。$$
$$(a)\enspace 0 < |z| < 1の時、|\frac{z}{i}| < 1より$$
$$f\left(z\right)=\frac{1}{z}・\frac{1}{-i\left(1-\frac{z}{i}\right)}$$
$$\left(1-\frac{z}{i}\right)の部分が無限等比級数の和の形になってますね。$$
$$f\left(z\right)=-\frac{1}{i}・\frac{1}{z}\left\{1+\left(\frac{z}{i}\right)+\left(\frac{z}{i}\right)^2+・・・\right\}$$
$$=\frac{i}{z}\displaystyle\left(1+\frac{z}{i}-z^2-frac{z^3}{i}+z^4+・・・\right)$$
$$=\frac{i}{z}+1-iz-z^2+iz^3+z^4-・・・$$
と展開できました。
$$(b) 1 < |z|の時、|\frac{i}{z}| < 1より、$$
$$f\left(z\right)=\frac{1}{z^2}・\frac{1}{1-\frac{i}{z}}$$
$$=\frac{1}{z^2}\left\{1+\left(\frac{i}{z}\right)+\left(\frac{i}{z}\right)^2+・・・\right\}$$
$$=\frac{1}{z^2}\displaystyle\left(1+\frac{i}{z}-\frac{1}{z^2}-\frac{i}{z^3}+\frac{1}{z^4}+・・・\right)$$
$$=\frac{1}{z-2}+\frac{i}{z^3}-\frac{1}{z^4}-\frac{i}{z^5}+・・・$$
と展開できました。
まとめ
今回はローラン級数について解説しました。
次回は留数について解説します。
ここまでご覧いただきありがとうございます。