今回は、極、留数、留数定理について解説して行きます。
複素関数 極
前回はローラン展開を解説しました。ちょっと復習しますと、
$$f\left(z\right)をローラン展開すると、以下のようになります。$$
$$f\left(z\right)=\displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}+\displaystyle\sum_{n=1}^{\infty}{\frac{b_n}{\left(z-z_0\right)^n}}$$
$$\displaystyle\sum_{n=1}^{\infty}{\frac{b_n}{\left(z-z_0\right)^n}}の部分を主要部と言いましたね。$$
$$ここで、主要部が$$
$$\displaystyle\sum_{n=1}^{m}{\frac{b_n}{\left(z-z_0\right)^n}}=\frac{b_1}{z-z_0}+\frac{b_2}{\left(z-z_0\right)^2}+・・・+\frac{b_m}{\left(z-z_0\right)^m}$$
$$のようになり、$$
$$有限の自然数mで主要部が表現できるとき、$$
$$z=z_0はm位の極と言います。$$
$$また、mが無限大の時、$$
$$z=z_0を真性特異点と言います。$$
留数
ここから留数についてお話しします。
$$複素関数f\left(z\right)をローラン展開すると、$$
$$f\left(z\right)=\displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}+\displaystyle\sum_{n=1}^{\infty}{\frac{b_n}{\left(z-z_0\right)^n}}$$
$$と表せて、a_n、b_nは、それぞれ$$
$$a_n=\frac{1}{2\pi i}\displaystyle\int_C\frac{f\left(z\right)}{\left(z-z_0\right)^{n+1}}dz\enspace\enspace\enspace\enspace(n=0, 1, 2, ・・・)$$
$$b_n=\frac{1}{2\pi i}\displaystyle\int_C\frac{f\left(z\right)}{\left(z-z_0\right)^{-n+1}}dz\enspace\enspace\enspace\enspace(n=1, 2, ・・・)$$
で与えられます。
$$ここで、b_1を留数と言います。$$
$$また、Res_{z=z_0}f\left(z\right)=b_1と書きます。$$
留数はresdiueなので、そのResですね。
$$ここで、f\left(z\right)の線積分について考えます。$$
コーシーの積分公式の記事の周回積分公式の証明の際も出てきた、
$$\displaystyle\int_C\left(z-α\right)^ndz=\displaystyle\begin{cases}2\pi i\left(n=-1\right) \\ 0\left(n≠-1\right) \end{cases}・・・①$$
の公式を思い出すと、
$$\displaystyle\int_Cf\left(z\right)dzの線積分の値は、$$
$$n=-1の時のみ値をもち、
$$それ以外は0となりました。$$
$$これを使って、\displaystyle\int_C f\left(z\right)dzを考えます。$$
$$\displaystyle\int_C f\left(z\right)dz$$
$$=\displaystyle\int_C\left\{ \displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}+\frac{b_1}{z-z_0}+\frac{b_2}{\left(z-z_0\right)^2}+・・・+\frac{b_n}{\left(z-z_0\right)^n}+・・・ \right\}dz$$
$$=\displaystyle\int_C\displaystyle\sum_{n=0}^{\infty}{a_n\left(z-z_0\right)^n}dz$$
$$+\displaystyle\int_C\frac{b_1}{z-z_0}dz+\displaystyle\int_C\frac{b_2}{\left(z-z_0\right)^2}dz+・・・+\displaystyle\int_C\frac{b_n}{\left(z-z_0\right)^n}dz+・・・$$
$$ここで、上で説明したように、$$
$$\displaystyle\int_C\left(z-α\right)^ndzの線積分の値は、$$
$$n=-1の時のみ値をもち、それ以外は0となるので、$$
$$\displaystyle\int_C\frac{b_1}{z-z_0}dz以外は全て0になります。$$
よって、
$$\displaystyle\int_C\left(z\right)dz=\displaystyle\int_C\frac{b_1}{z-z_0}dz=b_1\displaystyle\int_C\frac{1}{z-z_0}dz$$
$$となり、この計算は①の周回積分公式より、$$
$$\displaystyle\int_C f\left(z\right)dz=b_1\displaystyle\int_C\frac{1}{z-z_0}dz=2\pi ib_1=2\pi iRes_{z=z_0}f\left(z\right)$$
$$となります。$$
この結果からわかるように、
$$孤立特異点z=z_0の近傍を$$
$$正方向に1周する線積分には、留数のみ寄与されます。$$
留数定理
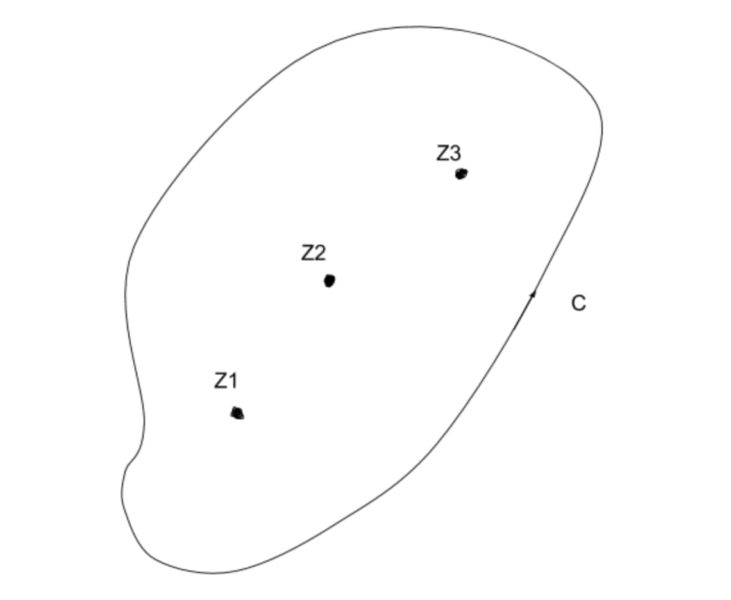
$$複素関数f\left(z\right)が単純閉曲線Cの内部で、$$
$$n個の特異点z_1、z_2、・・・、z_n$$
$$を除いて正則だとします。$$
$$また、そのn個の特異点のそれぞれの留数を$$
$$R_1、R_2、・・・、R_nとすると、$$
$$Cに対する線積分は、$$
$$\displaystyle\int_C f\left(z\right)dz$$
$$=2\pi i\displaystyle\sum_{k=1}^{n}Res_{z=z_k}f\left(z\right)$$
$$=2\pi i\left(R_1+R_2+・・・+R_n\right)$$
$$で与えられます。$$
留数定理 証明
$$証明$$
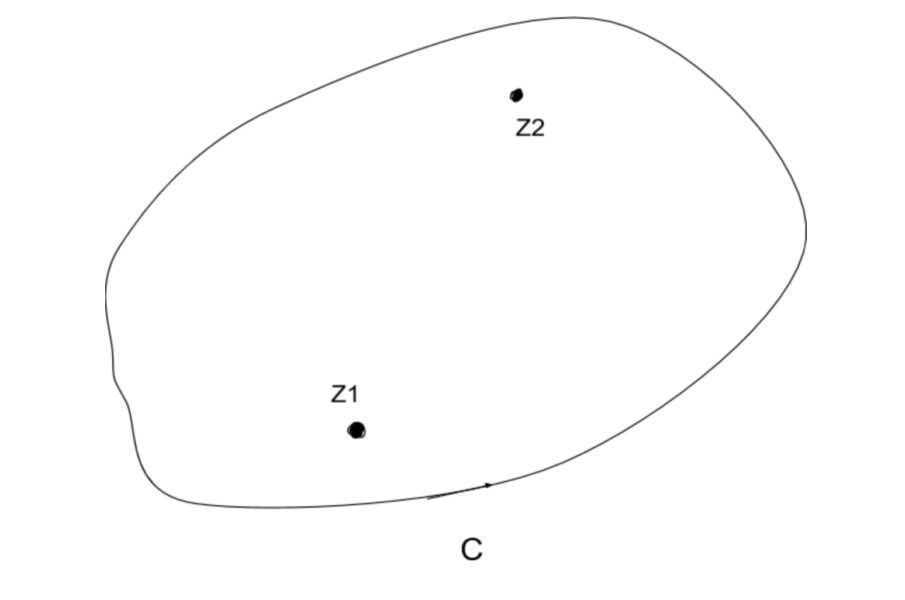
$$今、点z_1、z_2、・・・z_nは特異点で、$$
$$それら以外の点ではf\left(z\right)はCの内部で正則だとします。$$
ここで、コーシーの積分定理を思い出すと、
$$f\left(z\right)がその領域で正則な時はその領域内で、$$
$$積分経路を自由に変形できるのでした。$$

$$よって、図のように、$$
$$経路CをC'+C_1+C_2+・・・+C_nに変更します。$$
すると、
$$\displaystyle\int_C f\left(z\right)dz$$
$$=\displaystyle\int_{C'} f\left(z\right)dz+\displaystyle\int_{C_1} f\left(z\right)dz+\displaystyle\int_{C_2} f\left(z\right)dz+$$
$$・・・+\displaystyle\int_{C_n} f\left(z\right)dz・・・②$$
また、
$$C'は特異点を含まない正則な領域での線積分なので、$$
$$コーシーの積分定理より、$$
$$\displaystyle\int_{C'} f\left(z\right)dz=0$$
また、先ほど解説したように、
孤立特異点の近傍に1周する線積分には留数のみが寄与されます。
よって、
$$\displaystyle\int_{C_1} f\left(z\right)dz=2\pi iRes_{z=z_1}f\left(z\right)$$
$$\displaystyle\int_{C_2} f\left(z\right)dz=2\pi iRes_{z=z_2}f\left(z\right)$$
$$・・・$$
$$\displaystyle\int_{C_n} f\left(z\right)dz=2\pi iRes_{z=z_n}f\left(z\right)$$
となります。
したがって、
$$\displaystyle\int_C f\left(z\right)dz$$
$$=2\pi iRes_{z=z_1}f\left(z\right)+2\pi iRes_{z=z_2}f\left(z\right)+・・・+2\pi iRes_{z=z_n}f\left(z\right)$$
$$=2\pi i\displaystyle\sum_{k=1}^{n}Res_{z=z_k}f\left(z\right)$$
とできました。
留数の求め方
上では、留数を求めれば、簡単に線積分が求まることを解説しました。
では、留数はどのようにして求めるのでしょうか。
留数の定義を見ればわかるように、ローラン展開ができれば、
$$\left(z-z_0\right)^{-1}の係数が留数なので、すぐに求まります。$$
しかし、ローラン展開するのは非常にめんどうです。
違う方法で求めましょう。
$$留数の求め方$$
$$(i)\enspace1位の極の場合$$
$$Res_{z=z_0}f\left(z\right)=b_1=\lim_{z\to z_0}\left(z-z_0\right)f\left(z\right)$$
で求めます。
$$証明$$
$$f\left(z\right)をローラン展開すると、$$
$$f\left(z\right)=\frac{b_1}{z-z_0}+\displaystyle\sum_{n=0}^{\infty}{a_n}\left(z-z_0\right)^n$$
$$両辺に\left(z-z_0\right)をかける$$
$$\left(z-z_0\right)f\left(z\right)=b_1+\displaystyle\sum_{n=0}^{\infty}{a_n}\left(z-z_0\right)^{n+1}$$
$$z\to z_0の極限を求める$$
$$\lim_{z\to z_0}\left(z-z_0\right)f\left(z\right)=b_1$$
$$となりました。\displaystyle\sum_{n=0}^{\infty}{a_n}\left(z-z_0\right)^{n+1}は、$$
$$z\to z_0とすると0になりますね。$$
$$(ii)\enspace m位の極の場合$$
$$Res_{z=z_0}f\left(z\right)=b_1=\frac{1}{\left(m-1\right)!}\lim_{z\to z_0}\frac{d^{m-1}}{dz^{m-1}}\displaystyle\left[\left(z-z_0\right)^m f\left(z\right) \right]$$
で求めます。流れとしては、
$$f\left(z\right)に\left(z-z_0\right)^mをかけた関数を\left(m-1\right)回微分して、$$
$$z\to z_0の極限を求めて、\frac{1}{\left(m-1\right)!}をかけます。$$
$$証明$$
$$f\left(z\right)をローラン展開すると、$$
$$f\left(z\right)=$$
$$\frac{b_m}{\left(z-z_0\right)^m}+\frac{b_{m-1}}{\left(z-z_0\right)^{m-1}}+・・・+\frac{b_1}{z-z_0}+\displaystyle\sum_{n=0}^{\infty}a_n\left(z-z_0\right)^n$$
$$両辺に\left(z-z_0\right)^mをかけます。$$
$$\left(z-z_0\right)^m f\left(z\right)$$
$$=b_m+b_{m-1}\left(z-z_0\right)+・・・+b_1\left(z-z_0\right)^{m-1}$$
$$+\displaystyle\sum_{n=0}^{\infty}a_n\left(z-z_0\right)^{n+m}$$
両辺を微分します。(1回目)
$$\frac{d}{dz}\left[\left(z-z_0\right)^m f\left(z\right) \right]$$
$$=b_{m-1}+2b_{m-2}\left(z-z_0\right)+・・・+\left(m-1\right)b_1\left(z-z_0\right)^{m-2}$$
$$+\frac{d}{dz}\left[ \displaystyle\sum_{n=0}^{\infty}a_n\left(z-z_0\right)^{n+m} \right]$$
もう一度微分します。(2回目)
$$\frac{d^2}{dz^2}\left[\left(z-z_0\right)^m f\left(z\right) \right]$$
$$=2b_{m-2}+6b_{m-3}\left(z-z_0\right)+・・・+\left(m-1\right)\left(m-2\right)b_1\left(z-z_0\right)^{m-3}$$
$$+\frac{d^2}{dz^2}\left[ \displaystyle\sum_{n=0}^{\infty}a_n\left(z-z_0\right)^{n+m} \right]$$
(繰り返し)
もう一度微分します。((m-1)回目)
$$\frac{d^{m-1}}{dz^{m-1}}\left[\left(z-z_0\right)^m f\left(z\right) \right]$$
$$=\left(m-1\right)! b_1+\frac{d^{m-1}}{dz^{m-1}}\left[ \displaystyle\sum_{n=0}^{\infty}a_n\left(z-z_0\right)^{n+m} \right]$$
$$両辺のz\to z_0の極限を求めると、$$
$$lim_{z\to z_0}\frac{d^{m-1}}{dz^{m-1}}\left[\left(z-z_0\right)^m f\left(z\right) \right]=\left(m-1\right)! b_1$$
よって、
$$Res_{z=z_0}f\left(z\right)=b_1=\frac{1}{\left(m-1\right)!}lim_{z\to z_0}\frac{d^{m-1}}{dz^{m-1}}\left[\left(z-z_0\right)^m f\left(z\right) \right]$$
とできました。
例題(留数の求め方)
$$(i)\enspace f\left(z\right)=\frac{e^{iz}}{z+i}の留数$$
$$特異点は、z=-iで1位の極なので$$
$$Res_{z=-i}f\left(z\right)=\lim_{z\to -i}\left(z+i\right)f\left(z\right)$$
$$=\lim_{z\to -i}\left(z+i\right)\frac{e^{iz}}{z+i}$$
$$=\lim_{z\to -i}e^{iz}$$
$$=e$$
とできます。
$$(ii)\enspace f\left(z\right)=\frac{z^4}{\left(2z-i\right)^3}の留数$$
$$f\left(z\right)=\frac{z^4}{\left(2z-i\right)^3}=\frac{z^4}{8}・\frac{1}{\left(z-\frac{i}{2}\right)^3}$$
$$特異点は、z=\frac{i}{2}で3位の極なので、留数は、$$
$$Res_{z=\frac{i}{2}}f\left(z\right)=\frac{1}{\left(3-1\right)!}\lim_{z\to \frac{i}{2}}\left\{ \frac{d^{3-1}}{dz^{3-1}}\left(z-\frac{i}{2}\right)^3 f\left(z\right) \right\}$$
$$=\frac{1}{2!}\lim_{z\to \frac{i}{2}}\left\{ \frac{d^2}{dz^2} \left(z-\frac{i}{2}\right)^3・\frac{z^4}{8}・\frac{1}{\left(z-\frac{i}{2}\right)^3} \right\}$$
$$=\frac{1}{2}\lim_{z\to \frac{i}{2}}\left\{\frac{d^2}{dz^2}\displaystyle\left( \frac{z^4}{8} \right) \right\}$$
$$=\frac{1}{2}\lim_{z\to \frac{i}{2}}\displaystyle\left( \frac{3}{2}z^2 \right)$$
$$=\frac{1}{2}・\frac{3}{2}\displaystyle\left( \frac{i}{2} \right)^2=-\frac{3}{16}$$
とできます。
まとめ
今回は留数定理について解説しました。
留数定理は複素積分や次回お話しする実関数積分でも非常に役に立ちます。
次回は実関数積分について解説します。