今回は、ストークスの定理の意味と証明を解説していきます。
目次
ストークスの定理
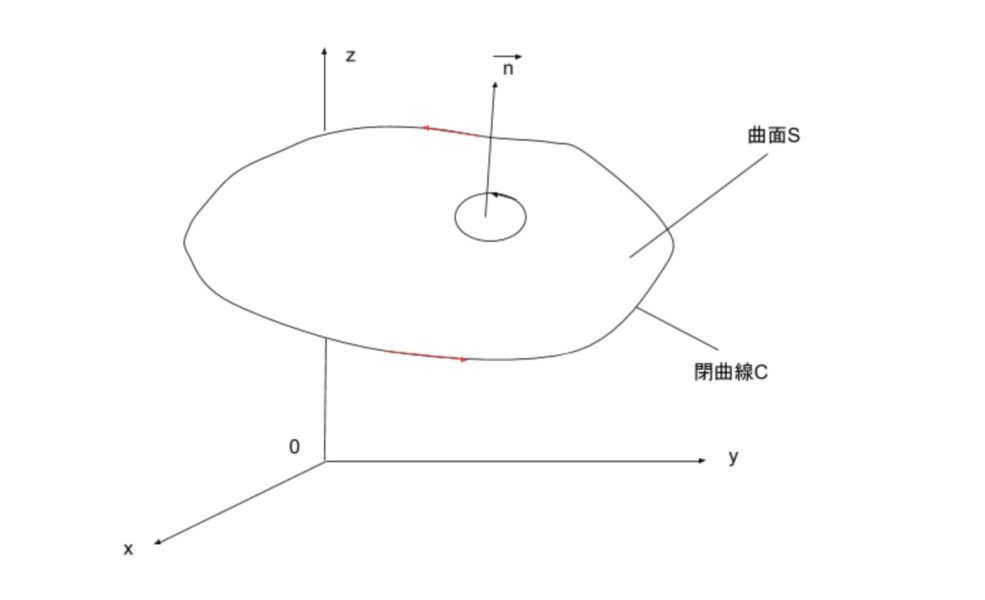
$$ある曲面Sにおいて、\vec{A}の面積分と、その曲面Sの端を経路とした\left(経路C\right)線積分について$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(∇\times\vec{A}\right)・d\vec{S}・・・①$$
$$が成り立ちます。$$
ストークスの定理の解釈
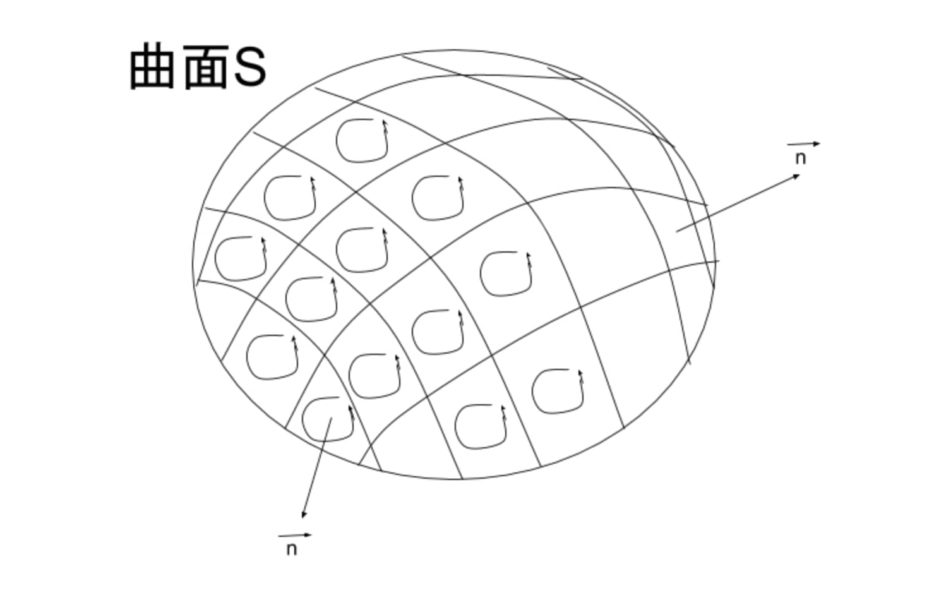
$$①の右辺について、$$
$$∇\times\vec{A}は、回転を表す。$$
回転の意味するものは、こちらの記事(勾配、発散、回転について)でも解説したように渦の強さでした。
$$①の右辺をみると、この回転と面積素ベクトル(d\vec{S}=\vec{n}dS)の内積を$$
$$積分計算していますから、上図のように、$$
$$無限個に分割した微小面積S_nそれぞれで回転を計算し、それらの合計と考えられます。$$
$$つまり、①の右辺は、微小面積S_nの法線ベクトル方向の回転の和を意味するということですね。$$
$$また、微小面積が隣り合っている部分は、回転(渦)の向きが逆で、互いに打ち消しあいます。$$
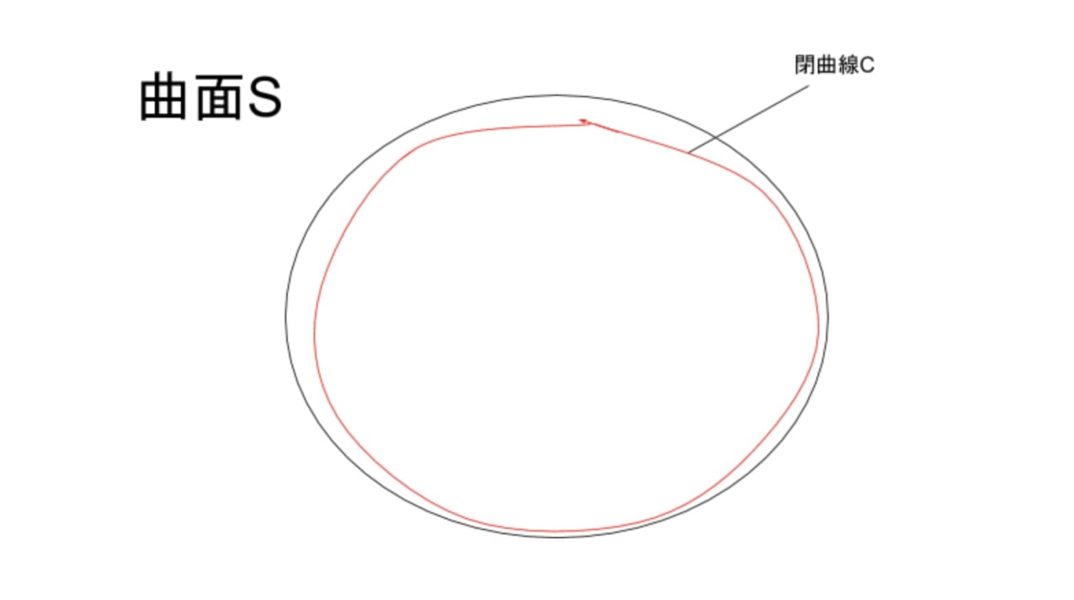
$$つまり、全体で考えると、その積分の値は、曲面Sの端の経路Cの周回積分と等しくなります。 $$
$$実際に、①の左辺は、経路をCとした\vec{A}の線積分となっているのがわかります。 $$
ストークスの定理の証明
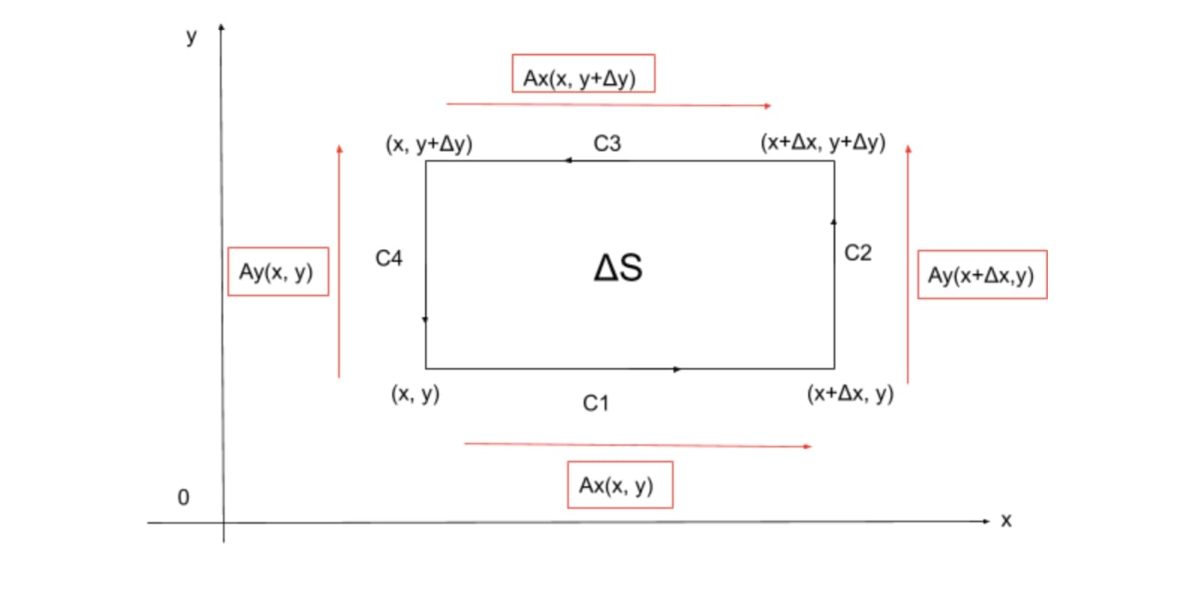
$$ここで、上図のように、xy平面上の横の長さがΔx、縦の長さがΔyの微小長方形を考えます。$$
$$①の左辺について$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r} = \displaystyle\int_{C_1}+\displaystyle\int_{C_2}+\displaystyle\int_{C_3}+\displaystyle\int_{C_4}$$
$$上のように、四つの経路に分解して見ます。$$
$$この四つの積分を計算していくのですが、まずは、C_1を例に具体的に考えてみましょう。$$
$$\displaystyle\int_{C_1}\vec{A}・d\vec{r}$$
$$経路C_1はx軸に平行なので、y成分は0と考え、\vec{A}・\vec{r}を計算します。$$
$$\vec{A}・\vec{r}=\left(A_x\left(x, y\right), 0\right)・\left(dx, 0\right)=A_x\left(x, y\right)dx$$
$$とできました。$$
$$A_x\left(x, y\right)dxは、A_x\left(x, y\right)が距離dxだけ仕事をした値とみることができます。$$
$$(力学で、仕事=力\times距離 みたいなイメージですね)$$
$$これを拡張して考えると、\displaystyle\int_{C_1}A_x\left(x, y\right)dxは、A_x\left(x, y\right)が$$
$$経路C_1の長さ分(Δx)だけ仕事をしたとできます。(直線経路だから単純で楽です)$$
$$よって、$$
$$\displaystyle\int_{C_1}A_x\left(x, y\right)dx=A_x\left(x, y\right)Δx$$
$$となることがわかります。$$
$$C_1と同様にして、C_2、C_3、 C_4も計算すると、以下のようにできます。$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r} ={A_x}\left(x, y\right)Δx+{A_y}\left(x+Δx, y\right)Δy-{A_x}\left(x, y+Δy\right)Δx-{A_y}\left(x, y\right)Δy$$
$$これを整理すると、$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=-\left\{{A_x}\left(x, y+Δy\right)-{A_x}\left(x, y\right)\right\}Δx+\left\{{A_y}\left(x+Δx, y\right)-{A_y}\left(x, y\right)\right\}Δy$$
$$=-\frac{{A_x}\left(x, y+Δy\right)-{A_x}\left(x, y\right)}{Δy}ΔxΔy+\frac{{A_y}\left(x+Δx, y\right)-{A_y}\left(x, y\right)}{Δx}ΔxΔy$$
$$=-\frac{\partial A_x}{\partial y}dxdy+\frac{\partial A_y}{\partial x}dxdy$$
$$と変形することができました。最後の変形は、$$
$$偏微分の定義式\displaystyle\lim_{\Delta x\rightarrow 0}\frac{A_x\left(x+\Delta x,y,z\right)-A_x\left(x,y,z\right)}{\Delta x}=\displaystyle\frac{∂A_x}{∂x}を考えると理解しやすいと思います。$$
$$(\displaystyle\lim_{\Delta x\rightarrow 0}Δx=dx)$$
$$よって、まとめると、$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\left(-\frac{\partial A_x}{\partial y}+\frac{\partial A_y}{\partial x}\right)dxdy$$
$$とできました。ただこのままでは、微小長方形のままなので、曲面S分だけ面積分すると、$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)dxdy・・・③$$
$$ここで、$$
$$∇\times\vec{A}=\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z},\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)$$
$$なので、③の右辺の中身は、∇\times\vec{A}のz成分と一致していることがわかります。よって、$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(∇\times\vec{A}\right)_z・d\vec{S}$$
$$とできます。$$
$$今回は、xy平面の微小長方形を考えましたが、同様にして、yz平面、zx平面についても考えると、それぞれ$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(∇\times\vec{A}\right)_x・d\vec{S}、\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(∇\times\vec{A}\right)_y・d\vec{S}$$
$$と出てくるはずです。$$
$$以上のことから、ストークスの定理が成り立っていることが証明できました。$$
まとめ
ここまでご覧いただきありがとうございます。
今回は、ストークスの定理について解説しました。
次回は、グリーンの定理について解説していきますので、ぜひご覧ください!