今回は、グリーンの定理(3次元と2次元)の解釈とその証明を詳しく解説していきます。
また、証明で「ガウスの定理」、「ストークスの定理」を前提知識として用いるので、ガウスの定理とストークスの定理をいまいちわかっていないという方は、「ガウスの定理の意味と証明」、「ストークスの定理の意味と証明」をご覧いただいてからこの記事を読んでいただけると、より深い理解が期待できると思います!
目次
グリーンの定理(3次元)
$$スカラー関数(大きさのみで、方向を持たない)f\left(\vec{r}\right),g\left(\vec{r}\right)があるとき、$$
$$\displaystyle\int_{V}\left(f\Delta g-g\Delta f\right)dV=\displaystyle\int_{S}\left(f∇g-g∇f\right)・d\vec{S}・・・①$$
$$が成り立ちます。$$
$$ここでの\Deltaは、ラプラシアンのことで、\Delta = ∇^2 です。$$
$$ラプラシアンは、\Delta=\frac{\partial^2}{∂x^2}+\frac{∂^2}{∂y^2}+\frac{∂^2}{∂z^2}で計算できます。$$
グリーンの定理(3次元)は、ラプラシアンを含む体積積分を面積分に置き換えることのできる定理です。
グリーンの定理(3次元)の証明
次に証明をしていきます。
$$①の左辺の中身(f\Delta g-g\Delta f)は、$$
$$f\Delta g-g\Delta f = ∇・\left(f∇g-g∇f\right)$$
$$に変形できます。 $$
$$この変形は、実際に計算してみるとすぐ求まるので、各自計算してみてください!$$
$$(右辺を計算すると左辺が出てきます。)$$
$$実際に計算したものをこの記事の最後に載せておきます。必要であれば参考にしてください。$$
$$この変形を用いて、グリーンの定理(3次元)の左辺を$$
$$\displaystyle\int_{V}\left(f\Delta g-g\Delta f\right)dV=\displaystyle\int_{V}∇・\left(f∇g-g∇f\right)dV$$
$$とできます。$$
$$ここで、$$
$$ガウスの定理 \displaystyle\int_{S}\vec{A}・d\vec{S}=\displaystyle\int_{V}∇・\vec{A}dV$$
$$より、さらに変形して、$$
$$\displaystyle\int_{V}∇・\left(f∇g-g∇f\right)dV = \displaystyle\int_{S}\left(f∇g-g∇f\right)・d\vec{S}$$
$$とできます。よって、グリーンの定理(3次元)の右辺となったので、証明完了です。$$
グリーンの定理(2次元)
グリーンの定理(3次元)を、ガウスの定理を用いて証明しました。
次は、グリーンの定理(2次元)を解説していきます。
$$グリーンの定理(2次元)$$

$$xy平面上で単純閉曲線Cで囲まれた領域Sの二つのスカラー関数f\left(x, y\right)、g\left(x, y\right)について、$$
$$\displaystyle\int_{C}\left(fdx+gdy\right)=\displaystyle\int_{S}\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dS・・・➃$$
$$が成り立ちます。$$
グリーンの定理(2次元)の証明
$$xy平面において、ストークスの定理は、$$
$$\displaystyle\int_{C}\vec{A}・d\vec{r}=\displaystyle\int_{S}\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)dS$$
$$とかけます。$$
$$ここで、ストークスの定理の証明の時と同様に、xy平面で微小長方形を考えると、$$
$$\displaystyle\int_{C_n}\vec{A}・d\vec{r}=\displaystyle\int_{S_n}\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)dS・・・⑥$$
$$となります。$$
$$ここで、\vec{A}\left(x, y\right)=\left(f\left(x, y\right), g\left(x, y\right)\right)とおきます。$$
$$すると、\vec{A}・d\vec{r}=\left(f, g\right)・\left(dx, dy\right)=fdx+gdyとなります。$$
$$よって、⑥の左辺は、$$
$$\displaystyle\int_{C_n}\vec{A}・d\vec{r}=\displaystyle\int_{C_n}\left(fdx+gdy\right)$$
$$と変形できます。$$
$$よって、⑥の式は、$$
$$\displaystyle\int_{C_n}\left(fdx+gdy\right)=\displaystyle\int_{S_n}\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dS・・・⑦$$
$$(\vec{A}\left(x, y\right)=\left(A_x, A_y\right)=\left(f, g\right))$$
$$⑦の左辺について$$
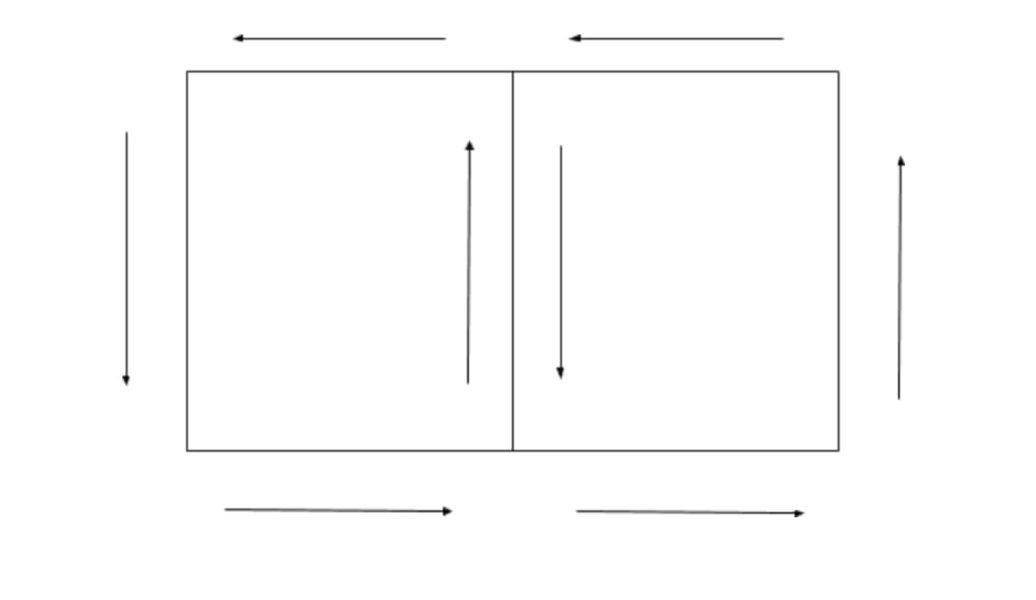
隣り合う微小長方形の接している部分は、互いに打ち消しあうため、全体で見ると、Cの線積分をすればいいことがわかります。
$$⑦の右辺について$$
微小長方形の面積分の和は、面積Sの面積分をすればいいだけなので、
$$⑦の式は、$$
$$\displaystyle\int_{C}\left(fdx+gdy\right)=\displaystyle\int_{S}\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dS$$
$$となり、グリーンの定理(2次元)が証明されました。$$
(補足)
$$f\Delta g-g\Delta f = ∇・\left(f∇g-g∇f\right) の計算$$
$$(右辺)= ∇・\left\{f\left(\frac{∂g}{∂x},\frac{∂g}{∂y},\frac{∂g}{∂z}\right)-g\left(\frac{∂f}{∂x},\frac{∂f}{∂y},\frac{∂f}{∂z}\right)\right\}$$
$$=∇・\left\{\left(f\frac{∂g}{∂x},f\frac{∂g}{∂y},f\frac{∂g}{∂z}\right)-\left(g\frac{∂f}{∂x},g\frac{∂f}{∂y},g\frac{∂f}{∂z}\right)\right\}$$
$$=∇・\left(f\frac{∂g}{∂x}-g\frac{∂f}{∂x},f\frac{∂g}{∂y}-g\frac{∂f}{∂y},f\frac{∂g}{∂z}-g\frac{∂f}{∂z}\right)$$
$$=\left(\frac{\partial}{∂x},\frac{∂}{∂y},\frac{∂}{∂z}\right)・\left(f\frac{∂g}{∂x}-g\frac{∂f}{∂x},f\frac{∂g}{∂y}-g\frac{∂f}{∂y},f\frac{∂g}{∂z}-g\frac{∂f}{∂z}\right)$$
$$ここからが少し面倒臭いのですよね。。$$
$$例として、x成分の内積結果を見てみます。$$
$$\frac{\partial}{∂x}\left(f\frac{∂g}{∂x}-g\frac{∂f}{∂x}\right)=\frac{\partial}{∂x}\left(f\frac{∂g}{∂x}\right)-\frac{\partial}{∂x}\left(g\frac{∂f}{∂x}\right)$$
$$上の二つの項それぞれに、積の微分公式を使います。$$
$$\frac{\partial}{∂x}\left(f\frac{∂g}{∂x}\right)-\frac{\partial}{∂x}\left(g\frac{∂f}{∂x}\right)=\left(\frac{∂f}{∂x}\frac{∂g}{∂x}+f\frac{∂^2g}{∂x^2}\right)-\left(\frac{∂g}{∂x}\frac{∂f}{∂x}+g\frac{∂^2f}{∂x^2}\right)$$
$$するとうまいことに、f\frac{∂^2g}{∂x^2}-g\frac{∂^2f}{∂x^2}だけが残ります。$$
$$同様にして、y成分、z成分も計算すると、$$
$$それぞれ、f\frac{∂^2g}{∂y^2}-g\frac{∂^2f}{∂y^2}、f\frac{∂^2g}{∂z^2}-g\frac{∂^2f}{∂z^2}が残ります。$$
$$これらを足し合わせると、$$
$$f\frac{∂^2g}{∂x^2}-g\frac{∂^2f}{∂x^2}+f\frac{∂^2g}{∂y^2}-g\frac{∂^2f}{∂y^2}+f\frac{∂^2g}{∂z^2}-g\frac{∂^2f}{∂z^2}$$
$$=f\left(\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}+\frac{∂^2}{∂z^2}\right)g-g\left(\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}+\frac{∂^2}{∂z^2}\right)f$$
$$=f\Delta g-g\Delta f$$
$$無事に左辺になってくれました!$$
$$ここまで読んでいただきありがとうございました!そしてお疲れ様です!$$
まとめ
ここまでご覧いただきありがとうございます。
今回はグリーンの定理を2次元、3次元の二種類に分けて解説しました。
次回からは、複素関数について解説していきますので、ぜひご覧ください!