今回は、ガウスの発散定理について解説していきます。
ガウスの定理
$$ある空間Vにおいてベクトル\vec{A}とその導関数が連続であるとき、$$
$$\displaystyle\int_{S}\vec{A}・d\vec{S}=\displaystyle\int_{V}∇・\vec{A}dV$$
$$が成り立ちます。$$

$$ここで、Sは空間Vの表面を表しています。$$
$$(左辺)のd\vec{S}は、「面積素ベクトル」のことで、d\vec{S}=\vec{n}dSと書けます。$$
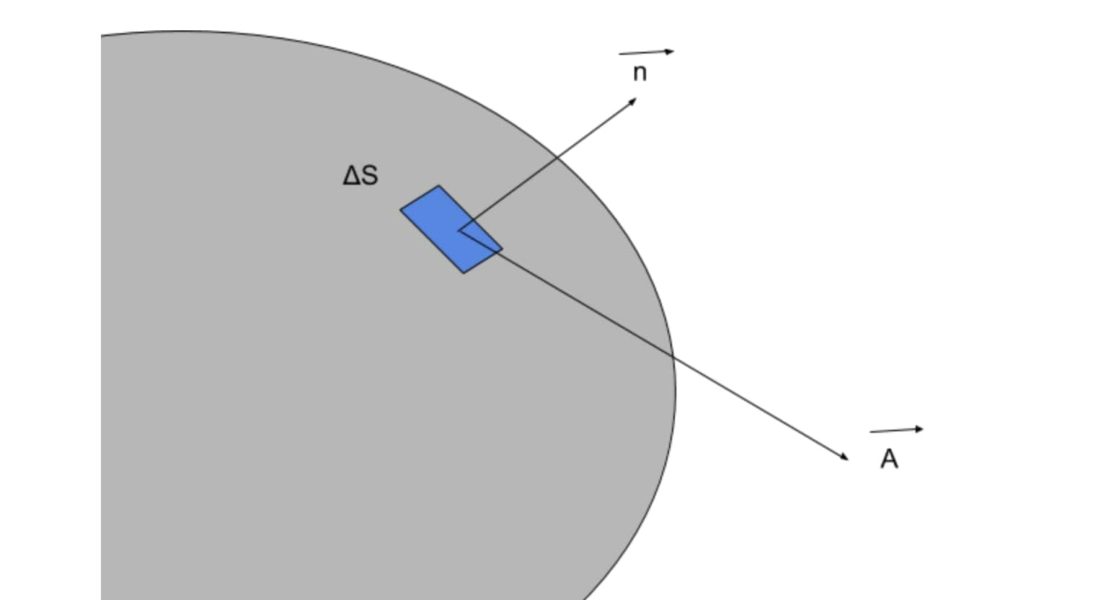
$$\vec{n}は、曲面上から出る法線ベクトルで、dSは面積素です。つまり、d\vec{S}は、$$
$$曲面上の微小な面積Sの大きさとその曲面の向きという二つの情報を持ちます。$$
ガウスの定理の解釈
上の式から、ガウスの定理は、
$$\displaystyle\int_{S}\vec{A}・d\vec{S}=\displaystyle\int_{V}∇・\vec{A}dV$$
$$「体積積分の値(右辺)は、その体積の表面のみの面積分の値(左辺)と等しい」・・・①$$
ということを表しています。
さらに詳しく見ていきます。
上の式の$$ ∇・\vec{A}$$ は、前回の記事(「勾配、発散、回転の意味」)で解説したように、
「発散」なので、
$$\left(∇・\vec{A}=div\vec{A}\right)$$
上の式は、以下のように変形できます。
$$\displaystyle\int_{S}\vec{A}・\vec{n}dS=\displaystyle\int_{V}div\vec{A}dV$$
この式から意味を解釈すると、
$$「曲面Sから\vec{A}が流出する総量 = 領域Vから\vec{A}が流出する総量」・・・②$$
となります。
$$②について詳しく説明すると、$$
左辺について、
$$\vec{A}と\vec{n}dS(=面積素ベクトルd\vec{S})(少し上で解説)の内積なので、$$
$$左辺は 「\vec{A}が曲面S全体からどれだけ流れ出ているか」 を示しています。$$
右辺について、
$$発散(div\vec{A})は、前の記事で説明したように「単位体積あたりのベクトルの流出量」なので、$$
$$右辺は、 「\vec{A}が領域V全体で、どれだけ流出しているか」 を示しています。$$
$$つまり、①、②をまとめると、$$
$$ガウスの定理は、$$
$$\vec{A}が曲面S全体から流れ出る総量(左辺の面積分の値)$$
$$が$$
$$\vec{A}が領域V全体から流れ出る総量(右辺の体積積分の値)$$
$$と等しくなるということです。$$
ガウスの定理の証明
ここまでガウスの定理の解釈を詳しく説明してきました。
では、ここからガウスの定理を証明していきます。
証明
$$空間Vを無限個の微小直方体ΔVに分解します。$$
$$このとき、微小直方体から流出する\vec{A}の量は、$$
$$\left(Δ・\vec{A}\right)ΔV$$
となります。これは、前回の記事の「発散」のところで詳しく説明しています。
ちなみに、前回の記事では、
「微小直方体の全ての面から単位時間当たりに出る流体の量は、
$$\left(\frac{∂A_x}{∂x}+\frac{∂A_y}{∂x}+\frac{∂A_z}{∂x}\right)\Delta x\Delta y\Delta z$$とわかる。」
と書かれてます。$$\Delta x\Delta y\Delta zはつまり\Delta Vということですね。$$
$$よって、微小直方体から流出する\vec{A}は、\left(Δ・\vec{A}\right)を微小直方体の体積V_n分だけ計算するので、$$
$$\displaystyle\int_{V_n}\left(∇・\vec{A}\right)dV$$
とできます。
$$また、微小直方体から流出する\vec{A}の量を面積分から考えると、$$
$$\displaystyle\int_{S_n}\vec{A}・d\vec{S}$$
と書けます。
$$S_nは微小直方体の表面を表し、つまり、上の式は、\vec{A}・d\vec{S}を微小直方体の表面積の分だけ$$
$$計算するということですね。$$
$$上で、微小直方体から流出する\vec{A}の量を体積分と面積分で求めましたが、$$
$$それらは当然等しいので、$$
$$\displaystyle\int_{V_n}\left(∇・\vec{A}\right)dV=\displaystyle\int_{S_n}\vec{A}・d\vec{S}・・・③$$
が成り立つ。
$$③の右辺について$$
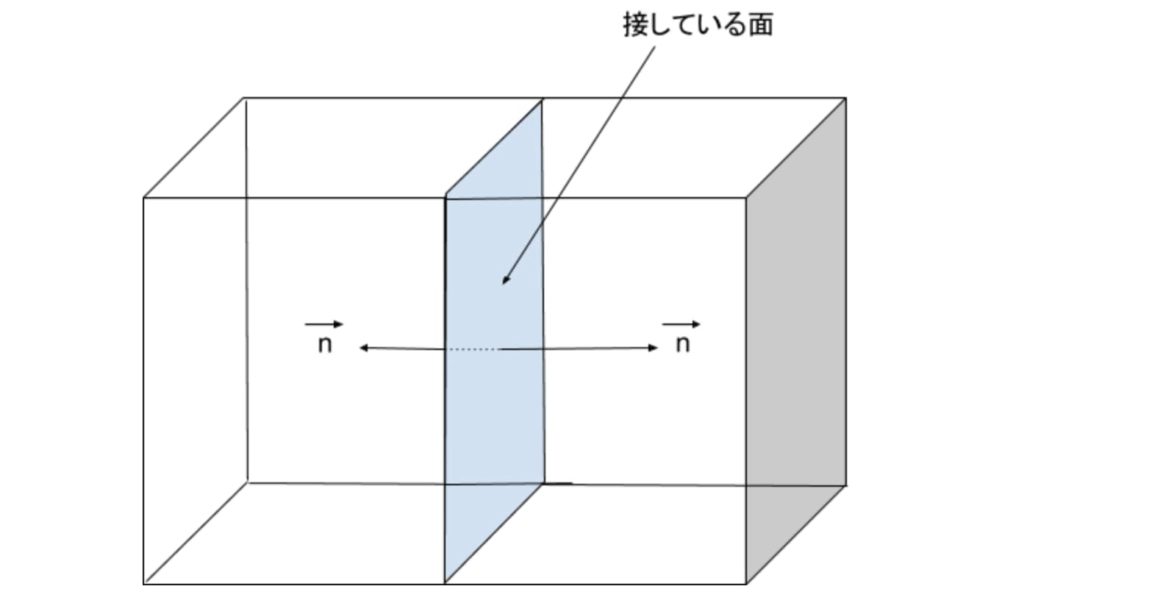
隣接する直方体が互いに接している面では、面の法線ベクトルの向きが逆向きとなり、接している面の面積分は消し合って計0となります。
このことを全体で考えると、微小直方体が合体してできた立体の表面積のみを考えれば良いことがわかります。
$$よって、微小直方体の面積分の合計は、$$
$$\displaystyle\sum_{n}{\displaystyle\int_{S_n}\vec{A}・d\vec{S}}=\displaystyle\int_{S}\vec{A}・d\vec{S}$$
とすることができます。
$$一方、③の左辺について$$
$$微小直方体の体積積分の和は、空間Vの体積積分とすればいいだけなので、$$
$$\displaystyle\sum_{n}{\displaystyle\int_{V_n}\left(∇・\vec{A}\right)dV}=\displaystyle\int_{V}\left(∇・\vec{A}\right)dV$$
とできます。よって、
$$\displaystyle\int_{S}\vec{A}・d\vec{S}=\displaystyle\int_{V}\left(∇・\vec{A}\right)dV$$
となり、ガウスの定理が証明されました。
まとめ
ここまで記事を読んでいただきありがとうございました。
今回は、「ガウスの定理」について解説しました。
ガウスの定理は、グリーンの定理の証明や、電磁気学など様々なところで役に立ちます。
今後ベクトル解析、複素解析、電磁気学など、たくさんの記事を作成していくので、一緒に物理の理解を深めていきましょう!