今回は、複素関数の極限、連続性、導関数について解説していきます。
まず、複素関数の極限を定義し、それを利用して、複素平面における複素関数の連続性と導関数を定義していきます。
複素関数の極限
まず複素関数の極限について定義していきます。
実関数での極限は、数直線上のある値に近づくことを言いましたが、複素関数では、
複素平面上のある値に近づく極限を考えます。
つまり、複素平面上で、その値にあらゆる方向から近づくということですね。
$$定義$$
$$複素数 z\to z_0のとき、複素関数 f\left(z\right)\to ω_0であるとき、$$
$$\lim_{z\to z_0}f\left(z\right)=ω_0$$
$$と書く。ここで、ω_0は複素関数f\left(z\right)の極限値という。$$
ここで再度注目したいのは、複素関数の極限は、方向によらないということですね。
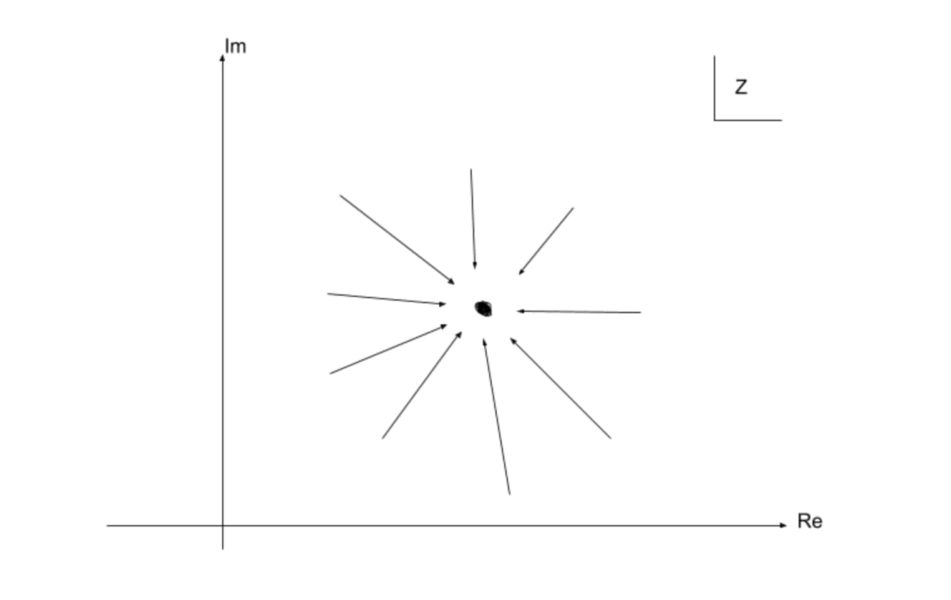
$$あらゆる方向から極限に近づくということです。$$
複素関数の連続性
上では、複素関数の極限を定義しました。
次に、複素関数の連続性を定義してみましょう。
$$定義$$
$$複素関数f\left(z\right)が、$$
$$\lim_{z\to z_0}f\left(z\right)=f\left(z_0\right)$$
$$であるとき、関数f\left(z\right)は、点z_0で連続であるという。$$
$$この定義の\lim_{z\to z_0}f\left(z\right)=f\left(z_0\right)は、$$
$$「f\left(z\right)という関数が、極限でz\to z_0に近づくとき、その値は、$$
$$f\left(z\right)にz=z_0を代入した値と一致するよ!」という意味ですね。$$
複素関数の導関数
複素関数の極限と連続性を定義できたので、導関数についても考えられそうです。
$$定義$$
$$複素関数f\left(z\right)について、以下の極限を考える。$$
$$f'\left(z_0\right)=\lim_{z\to z_0}\frac{f\left(z\right)-f\left(z_0\right)}{z-z_0}=\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$この値が存在するとき、これを複素関数f\left(z\right)の導関数という。$$
極限のところで説明したように、ここでも極限の近づき方は、方向によらず、複素平面上であらゆる方向から近づくことを意味します。
$$実関数の極限で、「xが+(プラス)から0に近づくとき」と$$
$$「xがー(マイナス)から0に近づくとき」を考えたのを覚えているでしょうか。$$
実関数では、この二つの極限の値が異なるとき、導関数は存在しない(その点で微分はできない)ということでしたね。
ここで、複素関数では、極限はあらゆる方向から近づく(方向に依存しない)ということでした。
つまり、言い換えれば、
$$複素関数の極限値が方向に依存するとき、導関数は存在しない$$
ということですね。
$$では、例として、f\left(z\right)=z^2の導関数を計算してみましょう。$$
$$f'\left(z\right)=\lim_{Δz\to 0}\frac{\left(z+Δz\right)^2-z^2}{Δz}$$
$$=\lim_{Δz\to 0}\frac{z^2+2zΔz+\left(Δz\right)^2-z^2}{Δz}$$
$$=2z$$
となります。
$$\left(Δz\right)^2=0として計算しています。$$
$$Δzはもともと微小な値として扱っていますから、その2乗ですから、無視してしまっても大丈夫でしょう。$$
$$(0.001)^2=0.000001みたいな。これは0です。$$
上の例からわかるように、複素関数の導関数は、実関数の導関数と同じように計算することができます。
まとめ
今回は、複素関数の極限、連続性、導関数について解説しました。
今回は定義の話ばかりだったので、あまり、詳しくお話しすることができませんでしたが、「こういうものなんだ」と考えていただければ、今はいいと思います。
また、導関数については、定義だけで、「ではどういったときに微分可能なのか」という点には触れていません。
このテーマはとても大事で、次回にお話しする「コーシー・リーマンの方程式」で詳しくお話しします。
ここまでご覧いただきありがとうございました!