今回はグルサの定理について解説していきます。
証明ではコーシーの積分公式を使用します。コーシーの積分公式はこちらの記事で詳しく解説しています。
グルサの定理
$$複素関数f\left(z\right)が単純閉曲線Cとその内部で正則なとき、$$
$$f\left(z\right)はCの内部でn階微分可能であり、$$
$$f^{(n)}\left(z\right)も正則である。$$
$$f^{(n)}\left(z\right)は、f\left(z\right)のn階微分を表します。$$
$$また、C内部の任意の点z_0について、$$
$$f^{(n)}\left(z_0\right)=\frac{n!}{2\pi i}\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0\right)^{n+1}}dz\enspace\enspace\enspace\enspace(n=1, 2, 3, ・・・)$$
$$\displaystyle\left(\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0\right)^{n+1}}dz=\frac{2\pi i}{n!}f^{(n)}\left(z_0\right)\enspace\enspace\enspace\enspace(n=1, 2, 3, ・・・)\right)$$
$$が成り立つ。$$
微分を求めたら積分が求まるというすごい定理ですね。
グルサの定理 証明
$$十分小さなΔzに対して次の式を考えます。$$
$$\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$これはΔz\to 0にしたら、完全にf'\left(z_0\right)ですね。$$
$$この式を変形していきましょう。$$
$$\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}=\frac{f\left(z_0+Δz\right)}{Δz}-\frac{f\left(z_0\right)}{Δz}・・・①$$
ここで、コーシーの積分公式
$$f\left(z_0\right)=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{z-z_0}dz$$
より、
$$f\left(z_0+Δz\right)=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{z-\left(z_0+Δz\right)}dz$$
$$f\left(z_0\right)=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{z-z_0}dz$$
$$と変形できるので、$$
$$①は、$$
$$\frac{f\left(z_0+Δz\right)}{Δz}-\frac{f\left(z_0\right)}{Δz}$$
$$=\frac{1}{2\pi iΔz}\displaystyle\oint_C\left(\frac{f\left(z\right)}{z-z_0-Δz}-\frac{f\left(z\right)}{z-z_0}\right)$$
$$=\frac{1}{2\pi iΔz}\displaystyle\oint_C\frac{\left(z-z_0\right)f\left(z\right)-\left(z-z_0-Δz\right)f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)}dz$$
$$=\frac{1}{2\pi iΔz}\displaystyle\oint_C\frac{\left(z-z_0\right)f\left(z\right)-\left(z-z_0\right)f\left(z\right)+Δzf\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)}dz$$
$$=\frac{1}{2\pi iΔz}\displaystyle\oint_C\frac{Δzf\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)}$$
$$=\frac{1}{2\pi i}\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)}$$
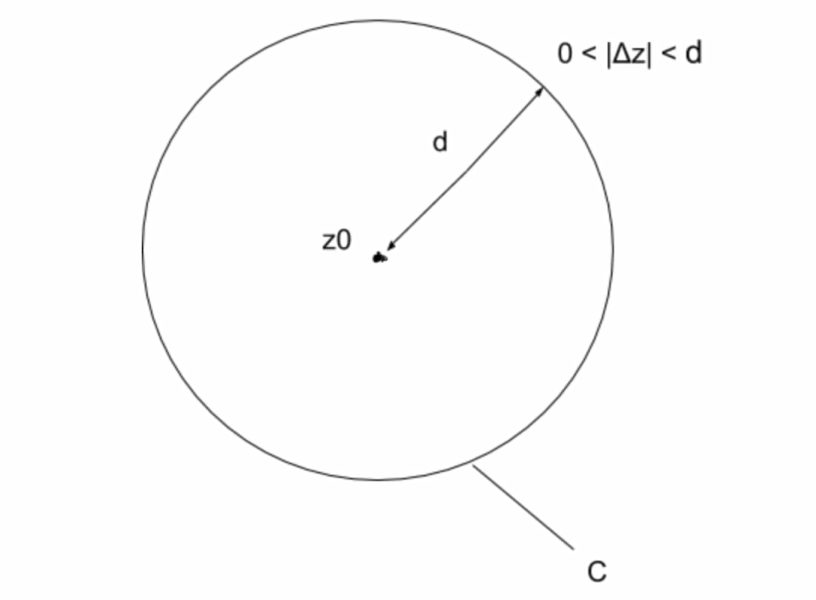
$$ここで、図のように、$$
$$経路Cはz=z_0を中心とする半径dの円とおきます。$$
$$また、Iを次のように定義します。$$
$$I=\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}-\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{\left(z-z_0\right)^2}dz・・・②$$
$$=\frac{1}{2\pi i}\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)}-\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{\left(z-z_0\right)^2}dz$$
$$=\frac{1}{2\pi i}\displaystyle\oint_C\frac{\left(z-z_0\right)f\left(z\right)-\left(z-z_0-Δz\right)f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)^2}dz$$
$$=\frac{1}{2\pi i}\displaystyle\oint_C\frac{\left(z-z_0\right)f\left(z\right)-\left(z-z_0\right)f\left(z\right)+Δzf\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)^2}dz$$
$$=\frac{Δz}{2\pi i}\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)^2}$$
$$ここで、Iが0となることを示せれば、$$
$$②より、グルサの公式が証明できそうです。$$
$$Iの絶対値を見てましょう。$$
$$|I|=\displaystyle\left\|\frac{Δz}{2\pi i}\displaystyle\oint_C\frac{f\left(z\right)}{\left(z-z_0-Δz\right)\left(z-z_0\right)^2}dz\right\|$$
$$≦\frac{|Δz|}{2\pi}\displaystyle\oint_C\frac{|f\left(z\right)|}{|z-z_0-Δz||z-z_0|^2}|dz|・・・③$$
$$ここで、$$
$$経路Cはz=z_0を中心とする半径dの円なので、$$
$$z=z_0+de^{iθ}、dz=die^{iθ}とできますね。$$
$$また、半径dの円なので、$$
$$|z-z_0|=d・・・➃$$
$$また、|f\left(z\right)|について、$$
$$f\left(z\right)の取りうる最大値をMとおくと、$$
$$|f\left(z\right)|≦M・・・⑤$$
$$ですね。➃、⑤より、③をさらに評価していきます。$$
$$\frac{|Δz|}{2\pi}\displaystyle\oint_C\frac{|f\left(z\right)|}{|z-z_0-Δz||z-z_0|^2}|dz|$$
$$≦\frac{|Δz|}{2\pi}\displaystyle\oint_C\frac{M}{\left(d-Δz\right)d^2}d dθ$$
$$=\frac{|Δz|}{2\pi}\displaystyle\frac{M}{\left(d-Δz\right)d}2\pi$$
$$=\displaystyle\frac{M}{\left(d-|Δz|\right)d}|Δz|$$
$$Iがいい感じにまとまりました。$$
$$ここで、Δz\to 0とすると、I\to 0となりますね。$$
$$よって、②より、$$
$$f'\left(z\right)=\displaystyle\lim_{Δz\to 0}\frac{f\left(z_0+Δz\right)-f\left(z_0\right)}{Δz}$$
$$=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f\left(z\right)}{\left(z-z_0\right)^2}dz$$
$$となり、グルサの定理のn=1の時が証明できました。$$
$$n≧2の時も同様に証明することができます。$$
まとめ
ここまでご覧いただきありがとうございます。
次回は、複素数の級数について解説します。