-

-
【Rails 初心者】日記投稿サービスを作る #1 インスタンス変数、HTTPメソッド
2021/3/17
みやちゃ 皆さんこんにちは、みやちゃです! 物理とプログラミングについて解説しています! 今回は「日記投稿サービスを作る」#1です。 これから順にRailsを詳しく解説していきながら、サービスを ...
-
-
ジョルダンの不等式の証明と例題 ジョルダンの方程式を利用して積分 【複素関数】
2021/3/19
今回はジョルダンの不等式について解説します。 この不等式は三角関数を含む定積分を求める際に便利な場合があります。 ジョルダンの不等式 $$\displaystyle\int_{0}^{\pi}e^{- ...
-
-
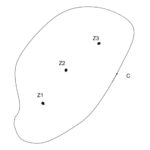
極 留数 留数定理 証明と例題 【複素関数】
2020/9/2
今回は、極、留数、留数定理について解説して行きます。 複素関数 極 前回はローラン展開を解説しました。ちょっと復習しますと、 $$f\left(z\right)をローラン展開すると、以下のようになりま ...
-
-
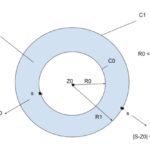
ローラン級数 証明 【複素関数】
2020/9/2
今回はローラン級数について解説します。 ローランの定理 $$図のように、$$ $$z_0を中心とする同心円のC_0(半径R_0)、$$ $$C_1(半径R_1)を考えます。$$ $$その円環領域で複素 ...
-
-
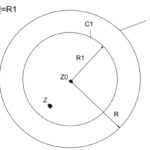
テイラー級数 証明【複素関数】
2020/9/2
今回は、実関数で度々登場したテイラー級数を複素関数に拡張します。 証明の際に「コーシーの積分公式」、「グルサの定理」を使用します。これらの公式は、「コーシーの積分公式」、「グルサの定理」で解説していま ...
-
-
グルサの定理 証明【複素関数】
2021/7/11
今回はグルサの定理について解説していきます。 証明ではコーシーの積分公式を使用します。コーシーの積分公式はこちらの記事で詳しく解説しています。 グルサの定理 $$複素関数f\left(z\right) ...
-

-
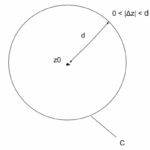
コーシーの積分公式 周回積分公式 証明【複素関数】
2020/9/2
前回は「コーシーの積分定理」について解説しました。 ちょっとだけ前回の復習をしますと、 $$単純閉曲線Cの内部において、複素関数f\left(z\right)が正則な時、Cに対する線積分は、0になる$ ...
-
-
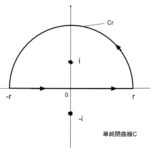
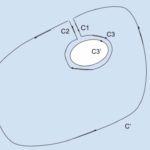
コーシーの積分定理 証明【複素関数】
2020/9/2
今回は複素平面上における積分のもっとも重要な定理の一つであるコーシーの積分定理を解説していきます。 また、証明では、「グリーンの定理」を用います。「グリーンの定理」がよくわからないという方は、こちらの ...
-
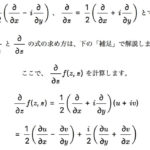
-
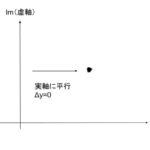
複素関数と正則性【複素関数】
2020/9/2
今回は、複素関数でもっとも大事な概念の一つの正則性について解説していきます。 複素関数が正則であるとは $$定義$$ $$複素関数f\left(z\right)が正則であるとは、$$ $$複素平面上の ...
-
-
コーシー・リーマンの方程式と微分可能性【複素関数】
2020/9/2
今回はコーシーリーマンの方程式と微分可能性について解説していきます。 前回の記事は複素関数の導関数についてで、複素平面上でも実数と同じように微分の考えを適応できるという話をしました。 そして、複素関数 ...