今回は複素平面上における積分のもっとも重要な定理の一つであるコーシーの積分定理を解説していきます。
また、証明では、「グリーンの定理」を用います。「グリーンの定理」がよくわからないという方は、こちらの記事で詳しく解説しているので、読んでいただけるとより深い理解が期待できると思います。
コーシーの積分定理

$$閉曲線Cとその内部で複素関数f\left(z\right)が正則な時、$$
$$ \displaystyle \oint_C f\left(z\right)dz =0$$
$$が成り立ちます。これをコーシーの積分定理と言います。$$
コーシーの積分定理の証明
$$証明$$
$$f\left(z\right)=u\left(x, y\right)+iv\left(x, y\right)とおきます。また、媒介変数tを用いて、$$
$$z\left(t\right)=x\left(t\right)+iy\left(t\right)とおくと、$$
$$\frac{dz}{dt}=\frac{dx}{dt}+i\frac{dy}{dt}とできるので、$$
$$\displaystyle \oint_C f\left(z\right)dz=\displaystyle\int\left(u\left(x, y\right)+iv\left(x, y\right)\right)\left(\frac{dx}{dt}+i\frac{dy}{dt}\right)dt$$
整理すると、
$$=\displaystyle\int\left(u\frac{dx}{dt}dt-v\frac{dy}{dt}dt\right)+i\displaystyle\int\left(u\frac{dy}{dt}dt+v\frac{dx}{dt}dt\right)$$
$$=\displaystyle\int\left(udx-vdy\right)+i\displaystyle\int\left(udy+vdx\right)・・・①$$
ここで、グリーンの定理 は、
$$\displaystyle\int_C\left(fdx+gdy\right)=\displaystyle\int_S\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dxdy$$
グリーンの定理は、線積分から面積分に変形できるのでしたね。
これを用いて、
$$①は、\displaystyle\int\left[\left(-\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+i\displaystyle\left(-\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}\right)\right]dxdy$$
と変形できます。
$$ここで、f\left(z\right)は閉曲線C上とその内部で正則だから、コーシー・リーマンの方程式を満たすので、①より、$$
$$\displaystyle \oint_C f\left(z\right)dz=0$$
$$となります。$$
よって、コーシーの積分定理が証明できました。
コーシーの積分定理によって得られる2つの定理
コーシーの積分定理によって、2つの定理が説明できます。
1、2点を結ぶ2つの線積分は等しい
$$定理$$
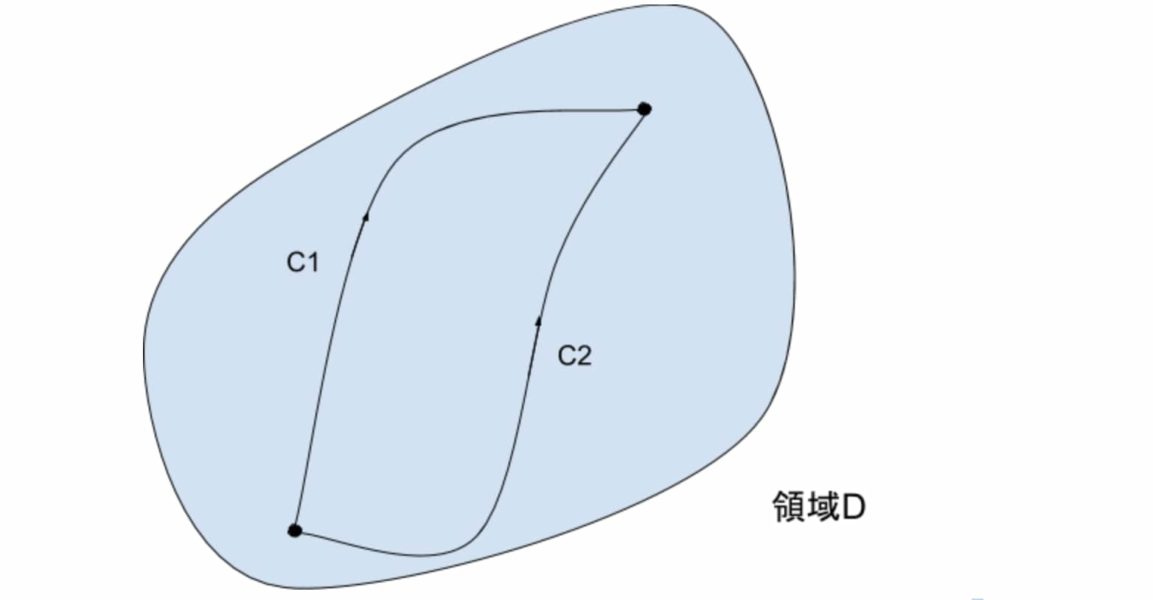
$$図のように、曲線C_1、C_2が領域D内で2点を結ぶ曲線で、$$
$$複素関数f\left(z\right)が領域Dで正則であるとき、2つの線積分は等しくなる。$$
$$\displaystyle\int_{C_1} f\left(z\right)dz=\int_{C_2}f\left(z\right)dz$$
$$証明$$
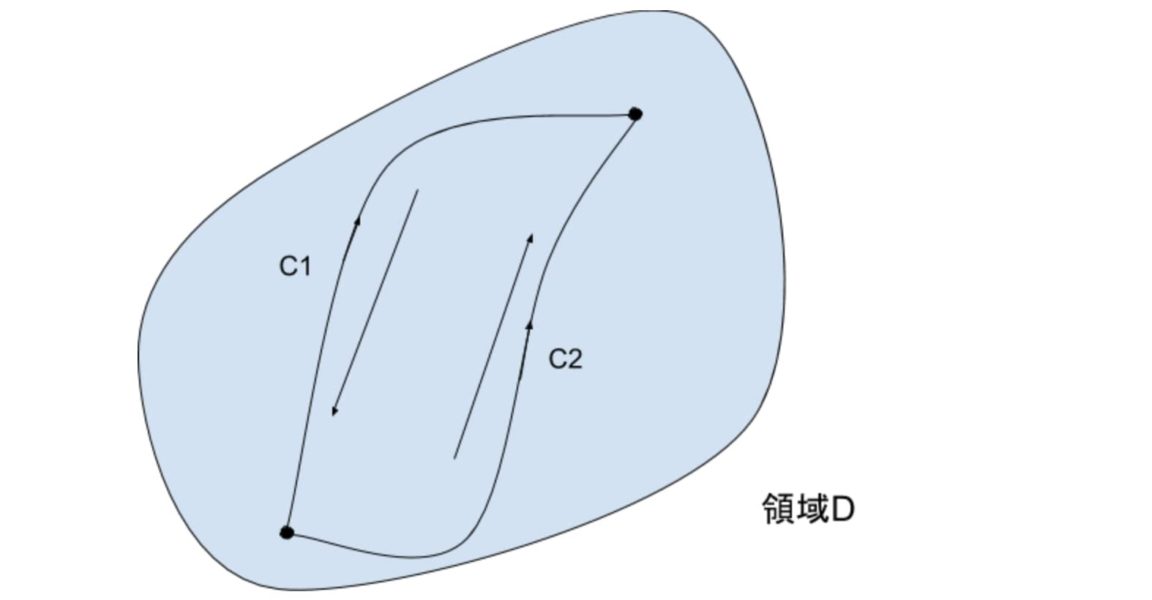
$$積分経路C=C_2-C_1を考えます。この経路は、図のようにC_2は正の方向(反時計回り)に、$$
$$C_1は負の方向に回ります。$$
$$積分経路Cは閉曲線であり、領域Dで複素関数f\left(z\right)は正則なので、$$
$$コーシーの積分定理より、$$
$$\displaystyle\int_{C_2-C_1}f\left(z\right)dz=0$$
$$である。よって、2つの線積分が等しいことが証明された。$$
$$簡単でしたね。$$
$$また、この定理から、$$
$$「正則な領域内では、複素関数に対する線積分は経路によらず、端点のみに依存する。」$$
$$つまり、積分経路は自由に変形可能だということがわかりました。$$
$$そこで、次の定理です。$$
2、積分経路は領域内で自由に変形可能
$$定理$$
$$複素関数f\left(z\right)が領域Dで正則である時、積分経路はD内で自由に変形することができる。$$
$$例を見てみましょう。$$
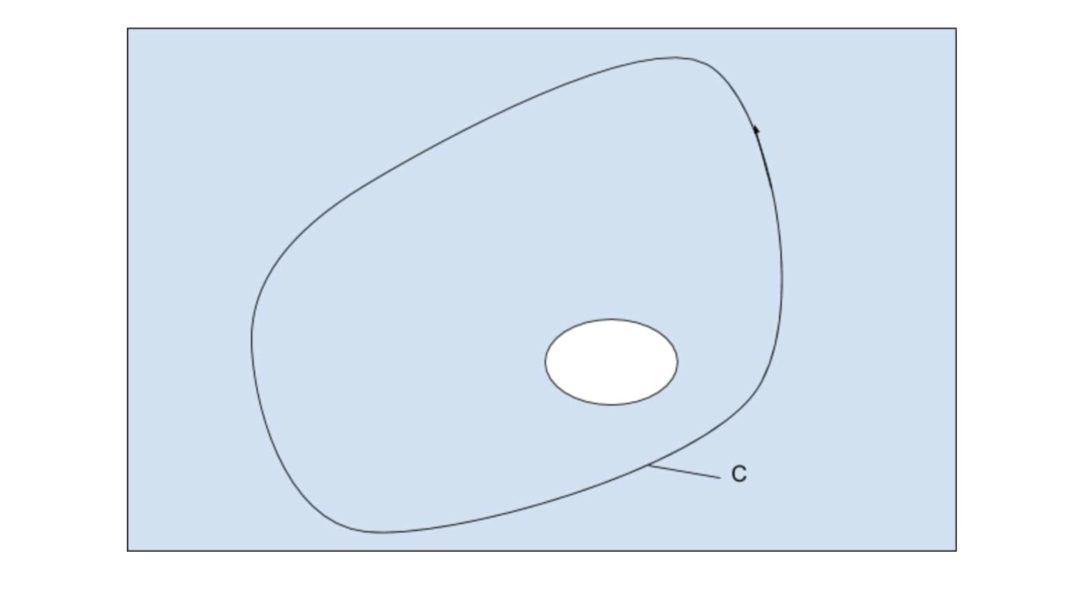
図のように、経路C内の中である領域のみ正則でない部分があります。(白い部分)
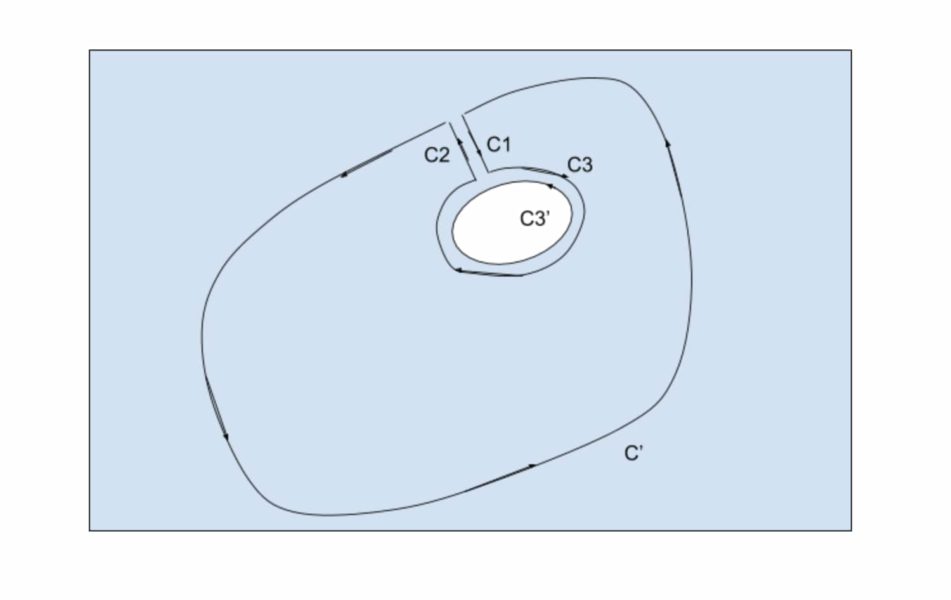
$$図のような経路を考えます。$$
$$C_1とC_2、C_3とC'_3はそれぞれ、経路が十分に近く、互いに方向が異なるので、$$
$$線積分の値が打ち消しあいます。$$
$$また、この経路は、うまく正則でない領域を避けてるので、コーシーの積分定理より、$$
$$経路C'+C_1+C_3+C_2に対する線積分はゼロとなる。$$
$$よって、$$
$$\displaystyle\int_C f\left(z\right)dz=\displaystyle\int_{C'+C_1+C_3+C_2}f\left(z\right)dz+\displaystyle\int_{C'_3}f\left(z\right)dz=\displaystyle\int_{C'_3}f\left(z\right)dz$$
$$となり、経路Cの線積分が、経路C'_3の線積分に変更できました。$$
まとめ
今回は、コーシーの積分定理と、それによって説明できる2つの定理について解説しました。
特に最後の経路を変形する手法は、今後かなりの頻度で使うことになると思います。
どんな気色の悪い経路にしようとも、それが正則な領域内であれば、全て0になるのは、なんかいいですね。
もちろん単純閉曲線になるように経路を変更しなければいけませんが。
次回は、「コーシーの積分公式」について解説します。
ここまでご覧いただきありがとうございます!