今回は、ベクトル解析の「勾配」、「発散」、「回転」の計算方法とその意味を解説していきます。
勾配
スカラー関数$$φ\left(x,y,z\right)$$の勾配は、
$$∇φ=\left(\frac{\partial}{∂x},\frac{∂}{∂y},\frac{∂}{∂z}\right)φ=\left(\frac{∂φ}{∂x},\frac{∂φ}{∂y},\frac{∂φ}{∂z}\right)$$
で計算できます。
$$φ\left(x,y,z\right)=a(定数)$$これは3次元空間中の平面を表します。

この時、$$∇φは、φ\left(x,y,z\right)=aに垂直であると言えます。$$
証明
$$φ\left(x,y,z\right)=a$$上を$$\vec{r}=\left(x,y,z\right)$$が動くとし、
ある座標における微小な変化を考えると、
$$d\vec{r}=\left(dx,dy,dz\right)$$
ここで、勾配と微小変化の内積を考えると、
$$∇φ・d\vec{r}=\frac{∂φ}{∂x}dx+\frac{∂φ}{∂y}dy+\frac{∂φ}{∂z}dz=dφ$$
となり、$$ここで、 φ\left(x,y,z\right)は一定の平面であるから、dφ=0、$$ $$つまり、∇φ・d\vec{r}=0であることがわかります。$$
$$したがって、∇φが面内のベクトルd\vec{r}と垂直であることが示されました。$$
発散
ベクトル場$$\vec{A}=\left(A_x,A_y,A_z\right)$$
の発散は、
$$div\vec{A}=∇・\vec{A}=\frac{∂A_x}{∂x}+\frac{∂A_y}{∂y}+\frac{∂A_z}{∂z}$$
で計算できます。
では、発散は何を意味するのでしょうか?
結論から言えば、
単位体積あたりのベクトルの流出量
です。

上図のような微小直方体ABCDEFGHに出入するベクトル(流体)を
$$x成分、y成分、z成分に分けて考えます。$$
$$x成分について$$
$$EFGHから入る流体の量は、A_x\left(x,y,z\right)のベクトルがEFGHの面積\Delta y\Delta zから入るから、$$
$$A_x\left(x,y,z\right)\Delta y\Delta z$$
とできます。
$$一方、ABCDから出る流体の量は、$$
$$A_x\left(x+\Delta x,y,z\right)のベクトルがABCDの面積\Delta y\Delta zから出るから、$$
$$A_x\left(x+\Delta x,y,z\right)\Delta y\Delta z$$
とできます。
$$よって、微小直方体のx軸方向に対して、流出する量は、$$
$$\left\{A_x\left(x+\Delta x,y,z\right)-A_x\left(x,y,z\right)\right\}\Delta y\Delta z=\frac{∂A_x}{∂x}\Delta x\Delta y\Delta z$$
とできます。
この変形は、偏微分の定義式
$$\displaystyle\lim_{\Delta x\rightarrow 0}\frac{A_x\left(x+\Delta x,y,z\right)-A_x\left(x,y,z\right)}{\Delta x}=\displaystyle\frac{∂A_x}{∂x}$$
これをみると、イメージできると思います。
$$x軸方向と同様にy軸方向、z軸方向も計算すると、それぞれ、$$
$$\frac{∂A_y}{∂x}\Delta x\Delta y\Delta z、\frac{∂A_z}{∂x}\Delta x\Delta y\Delta z$$
とできます。よって、微小直方体の全ての面から単位時間当たりに出る流体の量は、
$$\left(\frac{∂A_x}{∂x}+\frac{∂A_y}{∂x}+\frac{∂A_z}{∂x}\right)\Delta x\Delta y\Delta z$$とわかる。
$$また、単位体積あたりに出る流体の量は、\Delta x\Delta y\Delta zで割った$$
$$\frac{∂A_x}{∂x}+\frac{∂A_y}{∂x}+\frac{∂A_z}{∂x}\left(=∇・\vec{A}\right)$$
とできます。
回転
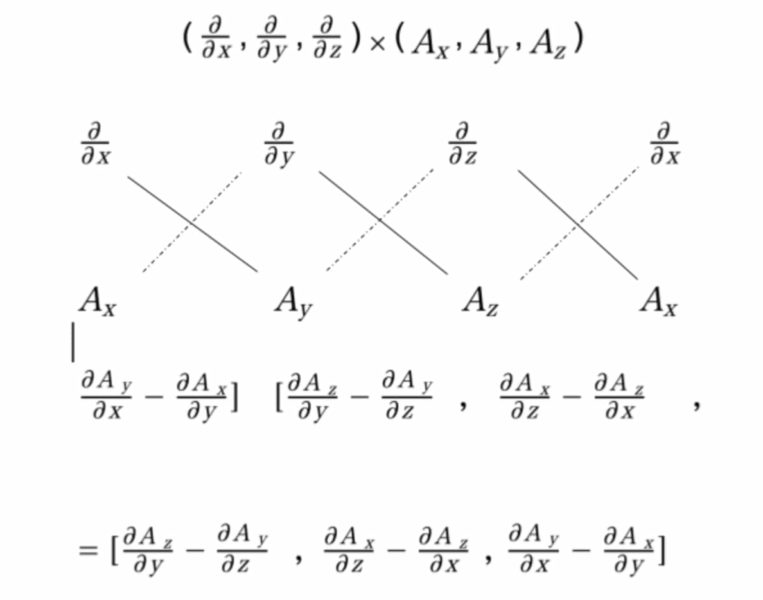
$$rot \vec{A}=∇\times\vec{A}=\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z},\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x},\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)$$
外積の計算は、下のように計算すると覚えやすいです。
回転は、ベクトル場の渦の強さを表します。
例を一つ挙げます。
$$位置ベクトル\vec{r}=\left(x,y,z\right)で角速度\vec{ω}=\left(0,0,ω\right) (ωは正の定数)の物体を考えます。$$
$$速度ベクトルは、\vec{V}=\vec{ω}\times\vec{r}で計算できるので、$$
$$\vec{V}=\left(-ωy,ωx,0\right)$$
となります。
速度ベクトルの大きさは、$$\left\|\vec{V}\right\|=ω\sqrt{x^2+y^2}$$
となり、
$$\sqrt{x^2+y^2}は原点からの距離を表すので、グラフでは、下のように動きます。$$

$$ここで、回転 ∇\times\vec{A}=\left(0,0,2ω\right) と計算でき、$$
$$回転 ∇\times\vec{A} はベクトル場 \vec{A} の渦の強さを表します。$$
まとめ
ここまでご覧いただきありがとうございました。
今回は、ベクトル解析の「勾配」、「発散」、「回転」について解説していきました。
初めは何をやっているのか、何に役立つのかがわからないという方も多いと思いますが、今後さらに深く物理を学ぶことで、これらのこともより深く理解ができると思います。