今回は、実関数で度々登場したテイラー級数を複素関数に拡張します。
証明の際に「コーシーの積分公式」、「グルサの定理」を使用します。これらの公式は、「コーシーの積分公式」、「グルサの定理」で解説しています。
テイラーの定理
$$z=z_0を中心とする半径Rの円Cの内部で$$
$$複素関数f\left(z\right)が正則である時、$$
$$f\left(z\right)=f\left(z_0\right)+f'\left(z\right)\left(z-z_0\right)+\frac{f''\left(z_0\right)}{2!}\left(z-z_0\right)^2+・・・・$$
$$=\displaystyle\sum_{n=0}^{\infty}{\frac{f^{\left(n\right)}\left(z_0\right)}{n!}\left(z-z_0\right)^n}$$
$$と展開できます。また、これをテイラー級数と言います。$$
テイラーの定理 証明
$$証明$$
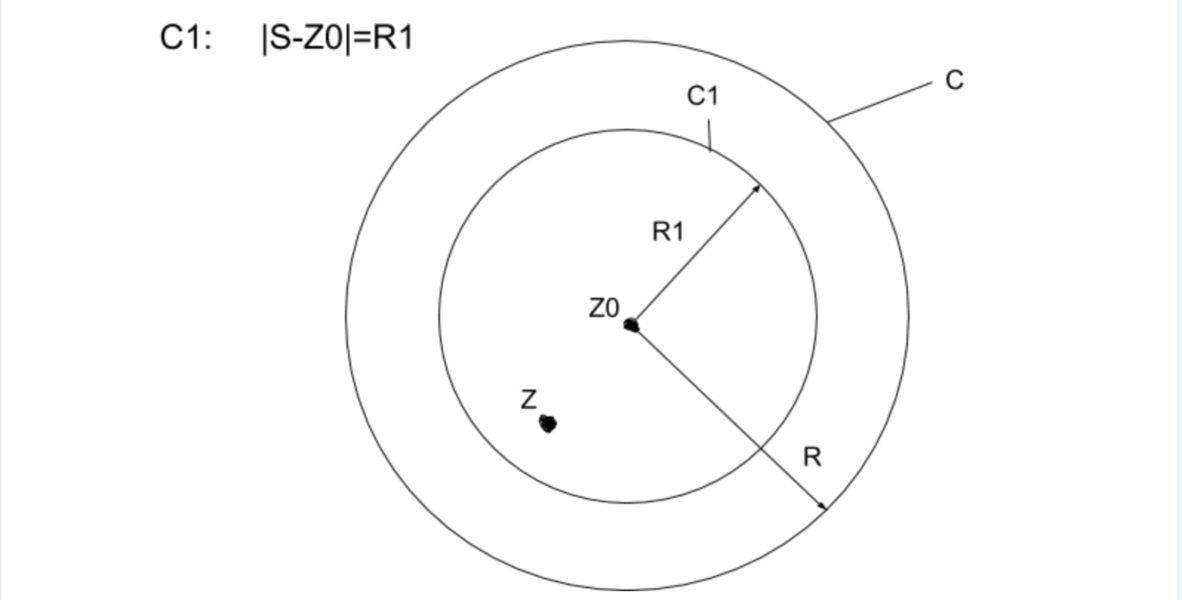
$$図のように、|s-z_0|=R_1の円C_1を考えます。$$
$$ここで、C_1の内部のzに注目し、コーシーの積分公式$$
$$f\left(z_0\right)=\frac{1}{2\pi i}\displaystyle\int_C\frac{f\left(z\right)}{z-z_0}dzより、$$
$$f\left(z\right)=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z}ds・・・①$$
と書けます。
$$①の\frac{1}{s-z}について$$
$$\frac{1}{s-z}=\frac{1}{s-z_0}\frac{1}{1-\frac{z-z_0}{s-z_0}}・・・②$$
$$と変形します。$$
$$これは、$$
$$\frac{1}{s-z_0}\frac{1}{1-\frac{z-z_0}{s-z_0}}=\frac{1}{s-z_0}\frac{1}{\frac{s-z_0-\left(z-z_0\right)}{s-z_0}}=\frac{1}{s-z}$$
$$とちゃんと元に戻りますね。$$
$$ここで、$$
$$初項1、公比r\left(|r| < 1\right)の無限等比級数の和は、$$
$$\displaystyle\sum_{n=0}^{\infty}{r^n}=1+r+r^2+r^3+・・・=\frac{1}{1-r}$$
$$とできるのでしたね。$$
$$②の\frac{1}{s-z_0}\frac{1}{1-\frac{z-z_0}{s-z_0}}は、この形なので、$$
$$|\frac{z-z_0}{s-z_0}| < 1 を示せれば、$$
$$いい感じに変形できそうです。$$
$$ここで、$$
$$点zは半径R_1の円C_1の内部で、$$
$$点z_0はC_1の中心です。$$
$$また、|s-z_0|=R_1なので、$$
$$|z-z_0| < |s-z_0|\left(=R_1\right)$$
$$\to |\frac{z-z_0}{s-z_0}| < 1 とできました。$$
$$よって、$$
$$\frac{1}{s-z_0}\frac{1}{1-\frac{z-z_0}{s-z_0}}=\displaystyle\sum_{n=0}^{\infty}{\left(\frac{z-z_0}{s-z_0}\right)^n}$$
$$と変形できます。よって、②より、$$
$$\frac{1}{s-z}=\frac{1}{s-z_0}\frac{1}{1-\frac{z-z_0}{s-z_0}}=\frac{1}{s-z_0}\displaystyle\sum_{n=0}^{\infty}{\left(\frac{z-z_0}{s-z_0}\right)^n}・・・③$$
$$③を①に代入しましょう。$$
$$①より、$$
$$f\left(z\right)=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z}ds$$
$$=\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{s-z_0}\displaystyle\sum_{n=0}^{\infty}{\left(\frac{z-z_0}{s-z_0}\right)^n}ds$$
$$=\displaystyle\sum_{n=0}^{\infty}\left(z-z_0\right)^n\frac{1}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{\left(s-z_0\right)^{n+1}}ds$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{\left(z-z_0\right)^n}{n!}\frac{n!}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{\left(s-z_0\right)^{n+1}}ds$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{f^{\left(n\right)}\left(z_0\right)}{n!}\left(z-z_0\right)^n$$
テイラー展開の式が無事出てきてくれました!
ちなみに、最後の変形は、グルサの定理より、
$$f^{\left(n\right)}\left(z_0\right)=\frac{n!}{2\pi i}\displaystyle\int_{C_1}\frac{f\left(s\right)}{\left(s-z_0\right)^{n+1}}dsを使用しました。$$
有名な関数のz=0周りのテイラー展開
$$e^z$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{1}{n!}z^n=1+z+\frac{1}{2}z^2+\frac{1}{6}z^3+・・・$$
$$cosz$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{\left(-1\right)^n}{\left(2n\right)!}z^{2n}=1-\frac{z^2}{2}+\frac{z^4}{24}-\frac{z^6}{720}+・・・$$
$$sinz$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{\left(-1\right)^n}{\left(2n+1\right)!}z^{2n+1}=z-\frac{z^3}{6}+\frac{z^5}{120}-\frac{z^7}{5040}+・・・$$
$$coshz$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{1}{\left(2n\right)!}z^{2n}=1+\frac{z^2}{2}+\frac{z^4}{24}+\frac{z^6}{720}+・・・$$
$$sinhz$$
$$=\displaystyle\sum_{n=0}^{\infty}\frac{1}{\left(2n+1\right)!}z^{2n+1}=z+\frac{z^3}{6}+\frac{z^5}{120}+\frac{z^7}{5040}+・・・$$
まとめ
今回は、テイラー級数について解説しました。
複素関数では、テイラー級数はある点の近傍で複素関数が正則でないと使用できませんでした。
正則でない領域を含み、テイラー展開ができない時には、ローラン級数を使用して展開します。
次回はローラン級数について解説します。